

Теория на экзамен 5 января 2006 г., группы 341-343.
1. (600) Определение термов конфигураций эквивалентных электронов в случае j-j связи. Определить энергию и функции основного терма р2 конфигурации в случае j-j связи. Функции выразить через сферические гармоники и спиновые функции электронов (a и b).
Ответ. Основной терм р2
конфигурации в случае j-j связи
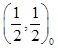 имеет энергию -2x, где x - константа
спин-орбитального взаимодействия для р-электронов. Так как для этого терма J = 0 и MJ = 0, он
невырожден, и его единственная функция имеет вид
имеет энергию -2x, где x - константа
спин-орбитального взаимодействия для р-электронов. Так как для этого терма J = 0 и MJ = 0, он
невырожден, и его единственная функция имеет вид

2. (600) Использование теории групп при определении разрешенных переходов в дипольном приближении. Определить будет ли увеличение числа разрешенных переходов (во всех поляризациях) при переходе от молекулярного иона Cu2+H3 (C3V группа) к иону Cu2+H6 (D3h группа).
Ответ. Для молекулярного иона Cu2+H3 (C3V группа) будет 7 разрешенных переходов (4 перехода с поляризацией XY, 1 переход Z и 2 перехода с XYZ поляризацией). Для молекулярного иона Cu2+H6 (D3h группа) будет 10 разрешенных переходов (6 переходов с поляризацией XY и 4 перехода поляризованы по Z).
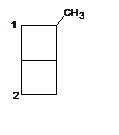
2. (200) Электрофильное замещение. Рассмотреть на примере реакции для p-системы, показанной на рисунке. Ориентирующее влияние оказывает индуктивный заместитель – CH3 –группа. Определить, по какому центру (1 или 2, указаны на рисунке) пойдет предпочтительнее реакция.
 Решение. В
первом порядке теории возмущений DEp
= qrDar . Из-за удаления
неспаренного электрона (электрофильное замещение) в оставшейся p-системы радикала (см. рисунок) q1 = q2 = q5 = 1, q3 = q4 = 1/2. и DEp3,4 = (1/2)xb, DEp1,2,5 = xb.
Барьер повышается при введении заместителя (xb > 0), поэтому предпочтительное
направление замещения по 3,4 центрам, что соответствует реакции по 2 центру на
первом рисунке.
Решение. В
первом порядке теории возмущений DEp
= qrDar . Из-за удаления
неспаренного электрона (электрофильное замещение) в оставшейся p-системы радикала (см. рисунок) q1 = q2 = q5 = 1, q3 = q4 = 1/2. и DEp3,4 = (1/2)xb, DEp1,2,5 = xb.
Барьер повышается при введении заместителя (xb > 0), поэтому предпочтительное
направление замещения по 3,4 центрам, что соответствует реакции по 2 центру на
первом рисунке.
4. (200) Термы линейных молекул. В линейной молекуле, относящейся к группе D¥h, в центре имеется атом с f-орбиталями. По какому представлению преобразуется в данной группе f-орбиталь этого атома, являющаяся Y30 сферической гармоникой?
Ответ. Неприводимое представление
![]() .
.
5. (400) Свойства циклических p-систем. Определить полную электронную энергию циклической p-системы из N p-центров, к одному из которых присоединен индуктивный заместитель CH3 группа.
Ответ. За счет снятия вырождения при введении индуктивного заместителя полная электронная энергия равна
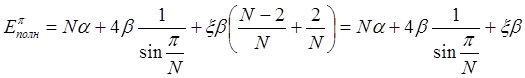 .
.
Задачи на экзамен 5 января 2006 г., группы 341-343.
1. (400) Для иона Ti3+ (электронная конфигурация 3d1) определить расщепление перехода 3d1 ® 4p1 (энергия Е0) в сильном магнитном поле с учетом слабого спин-орбитального взаимодействия. Указать число, поляризацию и энергии линий. Сколько всего переходов реализуется (энергии переходов могут и совпадать)?
Ответ. Переход 3d1 ® 4p1 (энергия Е0) в сильном магнитном поле с учетом слабого спин-орбитального взаимодействия расщепится на 5 линий с энергиями (в скобках указана поляризация)
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Всего будет 18 переходов, которые накладываясь друг на друга по энергии дадут 5 линий.
2. (400) Для системы из N электронов (N – четное число) определить количество значений Sполн = 0. Определить это число для N = 20.
Ответ. 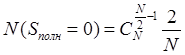 . Для N = 20
по этой формуле
. Для N = 20
по этой формуле ![]() .
.
3. (500) Определить функцию нижнего терма электронной конфигурации d2 с ML = 0.
Ответ. Три функции терма 3F с ML = 0 имеют пространственную функцию
![]() ,
которая умножается на 3 спиновые функции триплетного состояния (
,
которая умножается на 3 спиновые функции триплетного состояния (![]() ).
).
4. (400) Вырождение конфигураций ![]() и
и ![]() в 2 и 3
раза, соответственно, больше по сравнению с конфигурацией
в 2 и 3
раза, соответственно, больше по сравнению с конфигурацией ![]() . Определить величины l
и n.
. Определить величины l
и n.
Решение. Уравнения для нахождения параметров l и n имеют вид
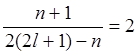 и
и 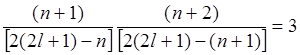 .
.
Из этих уравнений находим, что l =3 и n = 4, то есть это конфигурации f4, f5 и f6, вырождение которых равно 1001, 2002 и 3003, соответственно.
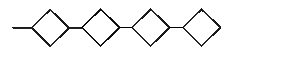
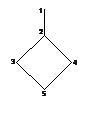
5. (300) Определить распределение спиновой плотности в p-радикале, представленном на рисунке.
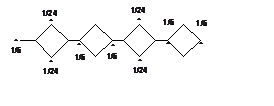 Ответ. На
втором рисунке представлено распределение спиновой плотности. Соотношение
коэффициентов определяется симметрией орбитали неспаренного электрона (b1 в группе C2v).
Ответ. На
втором рисунке представлено распределение спиновой плотности. Соотношение
коэффициентов определяется симметрией орбитали неспаренного электрона (b1 в группе C2v).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.