






Новосибирский Государственный Университет

Выполнила: Сахно Алина гр.3114
Преподователь: Аверина Т.А.
Постановка задачи и математические методы ее реализации
Рассматривается задача нахождения решения системы:
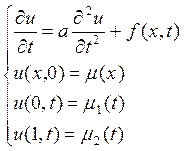
при начальных и граничных данных:
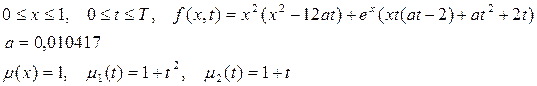
с помощью неявного метода Эйлера: 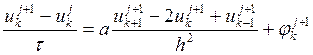
Известно так же точное решение: ![]() .
.
Необходимо 1. Исследовать схему на точность и устойчивость
2. Найти решение уравнения теплопроводности в узлах сетки
3. Вывести на экран графики точного и численного решений на каждом временном слое.
Неявный метод Эйлера
задается системой 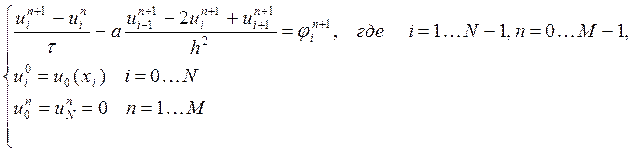
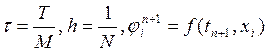
Поскольку метод неявный, то для нахождения решения исходной системы нужно решить СЛАУ на каждом временном слое. Матрица СЛАУ и столбец свободных коэффициентов восстанавливается по разностной схеме, начальным и граничным данным, таким образом система имеет вид:
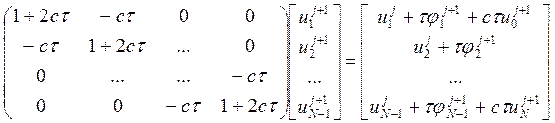
Решение системы производится методом прогонки, который заключается в сведении системы уравнений с трехдиагональной матрицей к системе с двухдиагональной матрицей.
Вычислим теперь погрешность аппроксимации и погрешность решения:
Мы получили, что ![]() , то есть при
, то есть при ![]() погрешность
стремится к нулю со скоростью
погрешность
стремится к нулю со скоростью ![]() .
.
Таким образом, неявный метод Эйлера безусловно устойчив.
ЧИСЛЕННЫЕ ЭКСПЕРИМЕНТЫ И АНАЛИЗ РЕЗУЛЬТАТОВ
h – шаг сетки по x, ![]() -
шаг сетки по t
-
шаг сетки по t
![]() -
ошибка
-
ошибка
Мы теоретически
установили, что точность решения О![]() , проверим это на
практике:
, проверим это на
практике:
|
|
|
|
|
|
|
|
Т.е. на самом деле при увеличении h в 2 раза ошибка увеличивается в 4 раза.
ИСПОЛЬЗУЕМАЯ ЛИТЕРАТУРА
1. Ж.Л.Коробицына, Г.С.Хакимзянов: Практикум на ЭВМ по курсу «Методы вычислений». Часть1 Разностные схемы для уравнений в частных производных с одной пространственной переменной
2. Лекции Лаевского Ю.М. по курсу «Методы вычислений»
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.