4. МЕТОДЫ РАСЧЕТА ПЕРЕХОДНОГО ПРОЦЕССА
Расчет переходного процесса связан с определением мгновенных значений переменных имитационной модели.
Математическое описание переходных процессов в общем случае может содержать независимые алгебраические уравнения, системы алгебраических уравнений и дифференциальные уравнения в форме Коши.
Алгебраические уравнения решаются последовательно и не требуют применения специальных вычислительных методов.
Для систем алгебраических уравнений с постоянными коэффициентами использован метод LU - разложения. Разложение матрицы коэффициентов на две треугольные осуществляется один раз на интервале неизменности структуры расчетной схемы. Для решения систем алгебраических уравнений с переменными коэффициентами использован метод Гаусса.
Интегрирование дифференциальных уравнений возможно методами второго и четвертого порядков.
Реализовано два метода второго порядка: метод Хойна и итетативный метод трапеций.
Если дифференциальное уравнение представить в виде
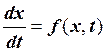 ,
,
то процедура метода Хойна описывается выражением:
![]() ,
,
где T - шаг интегрирования.
Этот метод называют также модифицированным методом трапеций.
Очевидно, что использование метода Хойна связано с двухкратным вычислением правой части системы дифференциальных уравнений на шаге интегрирования.
Если вычисления по приведенному выше выражению дополнить одной итерацией, т.е. вместо прогнозного значения функции, полученного по методу Эйлера, использовать результат применения исходной формулы, то получим итеративный метод трапеций.
Использование итеративного метода трапеций связано с трехкратным вычислением правых частей дифференциальных уравнений на каждом шаге интегрирования.
Точность интегрирования методом Хойна контролируется проверкой для каждой переменной условия: модуль разности прогнозного значения переменной, полученного по методу Эйлера, и значения переменной, полученного по методу Хойна, не больше произведения допустимой относительной погрешности расчета на характерное значение переменной.
Точность интегрирования методом трапеций контролируется аналогично, но вычисляется модуль разности прогнозного значения, полученного по методу Хойна, и значения переменной, полученного по методу трапеций.
В случае если на очередном шаге интегрирования хотя бы для одной функции указанное условие не выполняется, то выдается сообщение системы диагностики и расчет прекращается.
Следует отметить, что метод Хойна позволяет получить удовлетворительное по точности решение при шаге не более двух электрических градусов наивысшей воспроизводимой частоты, метод трапеций - при шаге не более 4 - 5 эл.градусов.
Из методов четвертого порядка реализованы метод Хемминга и Рунге-Кутта с постоянным шагом и метод Хемминга с переменным шагом. Использование метода Рунге-Кутта требует четырехкратного расчета правых частей дифференциальных уравнений на шаге интегрирования, метод Хемминга - два.
Точность интегрирования методом Хемминга с постоянным шагом контролируется проверкой для каждой переменной условия: модуль разности прогнозного и откорректированного значений переменной не более произведения допустимой относительной погрешности расчета на характерное значение переменной.
Точность интегрирования методом Рунге-Кутта не контролируется по причине значительных вычислительных затрат.
Точность интегрирования методом Хемминга с переменным шагом контролируется по суммарной погрешности. Реализован следующий способ определения значения суммарной погрешности, обеспечивающий выбор оптимального шага интегрирования: допустимая относительная погрешность расчета, задаваемая пользователем, делится на усредненную сумму величин, обратных характерным значениям интегрируемых переменных.
В случае, если требуемая точность расчета не будет обеспечена, то производится автоматическое изменение шага расчета в диапазоне до 1/1024 исходного шага. Если на очередном шаге интегрирования заданная точность не обеспечивается при минимально возможной величине шага, то выдается сообщение системы диагностики и расчет прерывается.
Следует отметить, что методы интегрирования четвертого порядка позволяют получить удовлетворительное решение даже при шаге в 25-30 эл. градусов наивысшей воспроизводимой частоты.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.