Моделирование нагрузки системы питания в операторном и физическом пространстве. Экспериментальная амплитудно-фазовая частотная характеристика звена

Пункт 1

Задание:

Представить нагрузку системы питания в виде звена, для которого входным сигналом является напряжение на зажимах источника питания, а выходным сигналом – указанная регулируемая переменная.

Исходная схема:

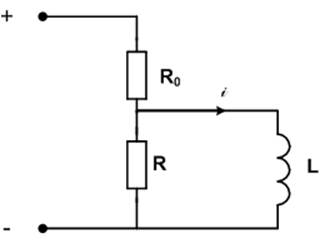
Решение этой задачи возможно двумя способами: в операторном и физическом пространстве, что даст нам возможность сделать проверку полученного результата, т.е. мы должны получить одно и тоже уравнение.

·  Решение в операторном пространстве.

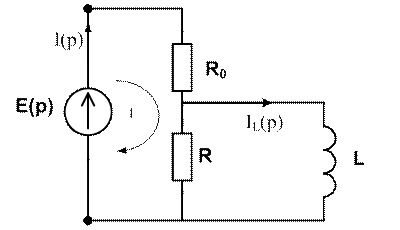
За входной сигнал примем :

 

За выходной сигнал примем ток катушки :

 

Найдем :

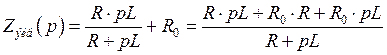
Зная , можем найти ток :

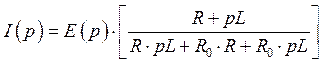
Запишем второй закон Кирхгофа по первому контуру, допуская, что напряжение на параллельных ветвях одинаково:

По закону Ома найдем :

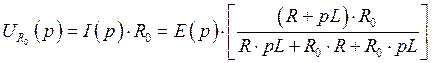
Подставим значение  и  в уравнение :

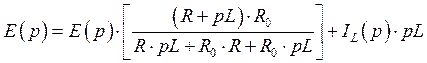
Произведем преобразования для получения конечной функции:

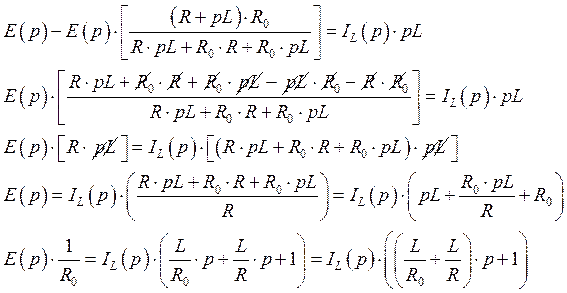
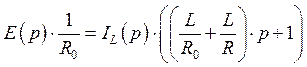
Конечное выражение имеет вид:

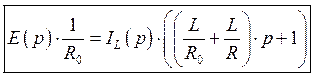
·  Решение в физическом пространстве.

Произведем расчет в физическом пространстве с теми же входными и выходными сигналами.

Исходная схема:

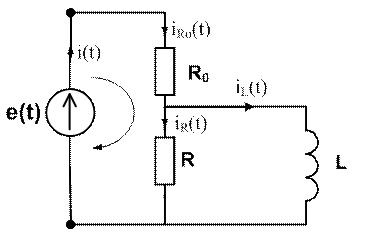
Составим систему уравнений по первому и второму закону Кирхгофа и добавим к ним уравнение напряжения катушки:

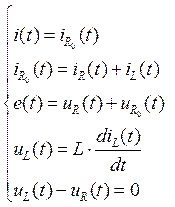
Преобразуем третье уравнение из системы до конечного вида:

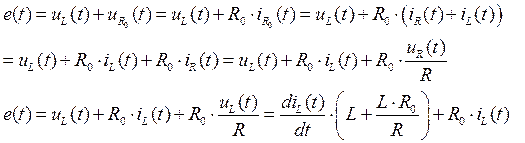
Конечное выражение имеет вид:

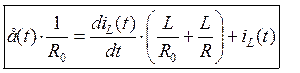
·  Проверка:

Если сделать замену 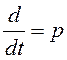, то последнее выражение принимает вид:

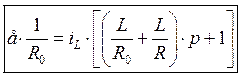
Следовательно, полученная формула верна.

Задание:

Получить описание звена в виде сокращённой записи дифференциального уравнения и передаточной функции. Установить тип звена и рассчитать численные значения параметров.

Сокращенная форма дифференциального уравнения – это отношение полинома воздействия к полиному реакции.

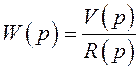
где 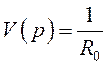 и 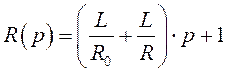. Подставим в формулу :

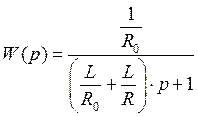
По передаточной функции можем определить тип: инерционное звено первого порядка, имеющее общий вид:

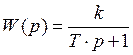
Рассчитаем численные значения параметров:

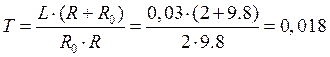
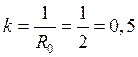
Пункт 2

Задание:

Определить двумя способами величину э.д.с. Е₀ основного источника:

 1) методом расчета установившегося режима системы питания и нагрузки;

2) используя передаточную функцию звена нагрузки. Э.Д.С. регулируемого источника Е_р в установившемся режиме принять равной нулю.

·  Метод расчета установившегося режима системы питания и нагрузки.

Исходная схема:

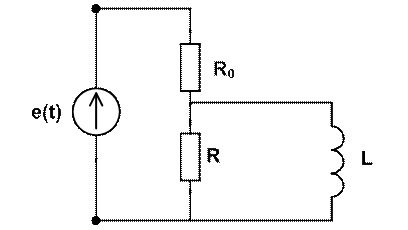
В установившимся режиме наша схема приобретет следующий вид:

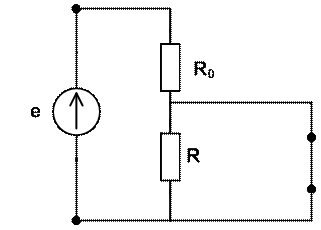
Преобразуем данную схему с учетом того, что резистор  зашунтирован.

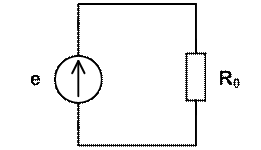
Найдем э.д.с.:

·  Используя передаточную функцию звена нагрузки.

По определению передаточная функция – это реакция звена на выходе при подаче на вход звена возмущения, т.е.:

  

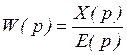
Отсюда:

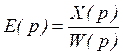
Нам надо найти . Зная свойство преобразования Лапласа:

Мы получаем следующее выражение:

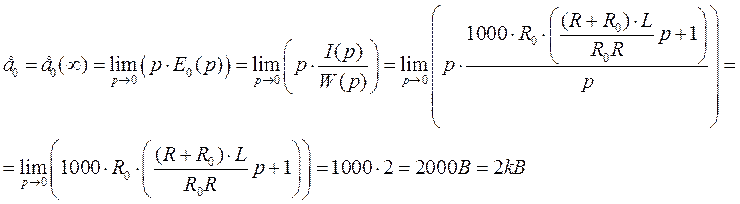
Полученные результаты совпали.

Пункт 3

Задание:

Построение аналитической переходной характеристики звена, эквивалентирующего нагрузку.

Переходная характеристика звена  представляет собой реакцию на выходе звена, вызванную подачей на его вход единичного ступенчатого воздействия, т.е. воздействие, которое мгновенно возрастает от нуля до единицы и далее остается неизменным.

Переходная характеристика звена   для нашего звена имеет вид:

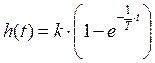
Подставим значение параметров:

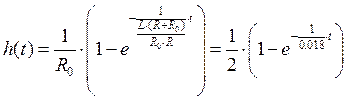
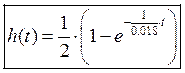
Построим данную кривую:

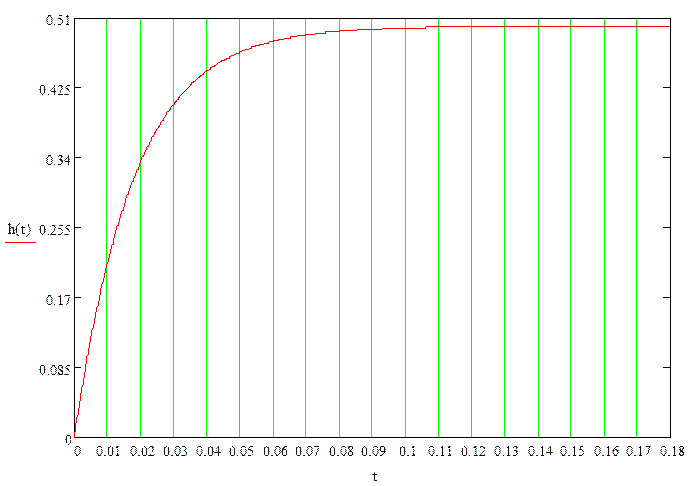
Пункт 4

Задание:

Подготовить имитационную модель и получить на ЭВМ переходную характеристику звена, эквивалентирующего нагрузку. Сравнить с результатами выполнения п.З. Определить параметры звена по экспериментальной переходной характеристике.

·  Подготовим имитационную модель.

В модель должны входить: генератор кусочно-постоянного сигнала и наше инерционное звено первого порядка, а так же для получения графика нам понадобятся осциллограф и табулятор. Схема модели имеет следующий вид:

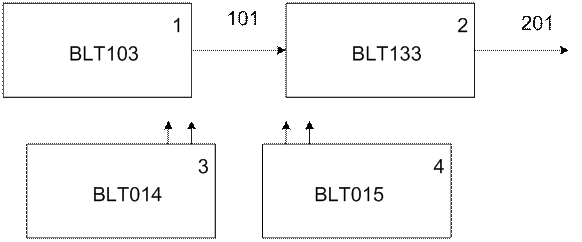
BLT103 – генератор кусочно-постоянного сигнала

BLT133 – инерционное звено первого порядка

BLT014 – осциллограф

BLT015 – табулятор

На осциллографе зададим два сигнала: 101 и 201.

Полученная осциллограмма:

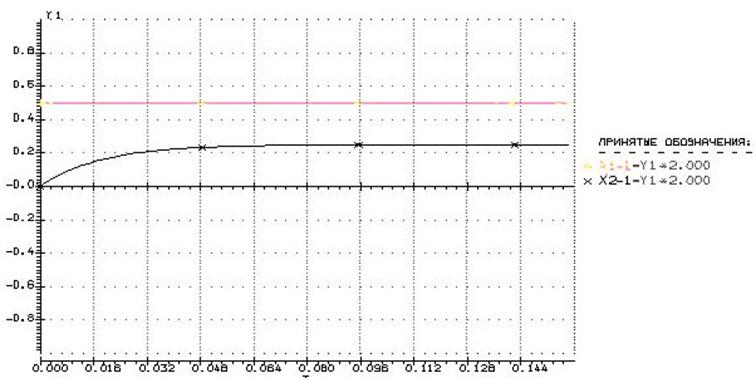
Полученные итоговые значения на табуляторе:

·  Обработка результатов:

Результаты, полученные из теоретического расчета:

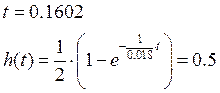
Результаты, полученные на табуляторе:

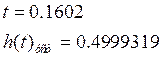
Расчет погрешности:

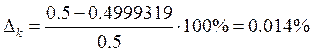
Погрешность в нахождение меньше процента, и ею можно пренебречь.

Для расчета  нам понадобится значения кривой до момента установившегося сигнала.

Возьмем любой момент времени и соответствующее ему значение кривой. Для этого в пункте “Обработки результатов” выберем “Таблицу мгновенных значений” и возьмем любую точку.

Полученная таблица:

  

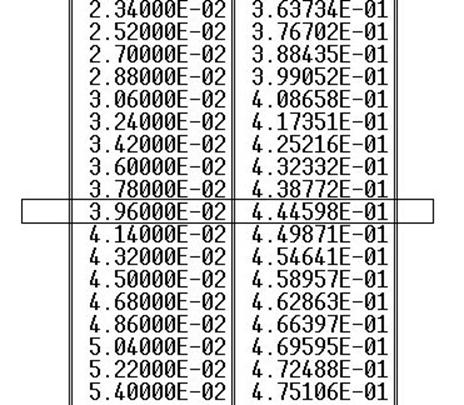
Наша точка:

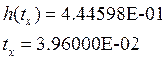
Тогда  можно выразить:

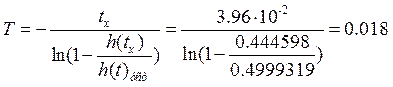
Пункт 5

Задание

Выполнить тестовый расчет, подтверждающий правильность определения величины э.д.с. Е₀.

Имитационная модель будет аналогичной при поиске переходной характеристики звена, за исключением заданного начального значения сигнала в блоке BLT103: в пункте 4 задана была единица по определению. Теперь же, необходимо задать рассчитанное значение э.д.с., что бы получить на выходе заданный ток.

Полученная осциллограмма:

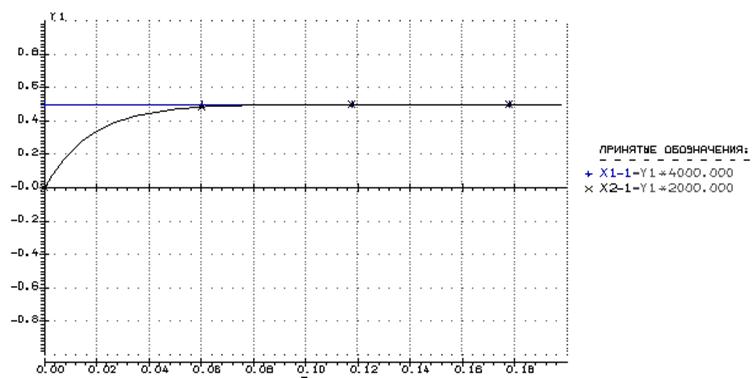
Данные полученные на табуляторе:

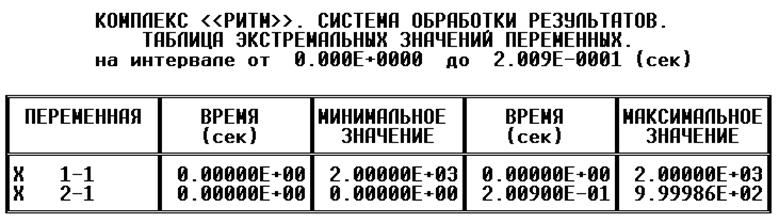
Найдем погрешность выполненного расчета.

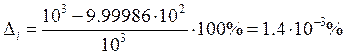
Погрешность меньше процента и, то есть, ей можно пренебречь, следовательно, на выходе получаем заданный ток, что говорит о правильности выполнения эксперимента.

Пункт 6

Задание:

Построить аналитическую амплитудно-фазовую частотную характеристику звена, эквивалентирующего нагрузку.

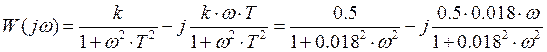
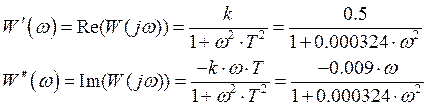
Построим зависимость :

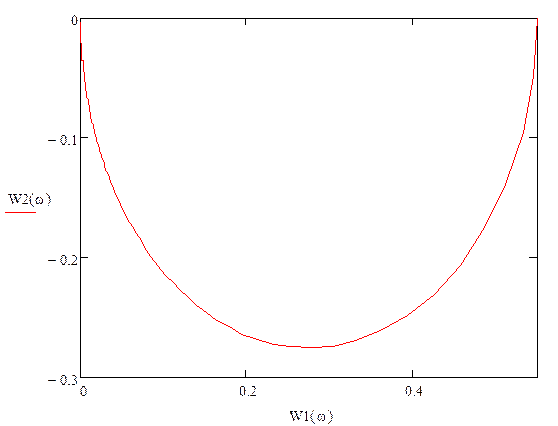
Пункт 7

Задание:

Подготовить имитационную модель и провести серию расчетов, позволяющую построить экспериментальную амплитудно-фазовую частотную характеристику звена, эквивалентирующего нагрузку. Сравнить с результатами выполнения пункта 6.

Проведем трассировку по данному графику и построим полученные точки:

 

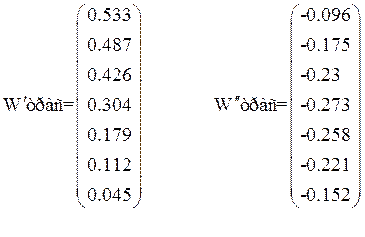
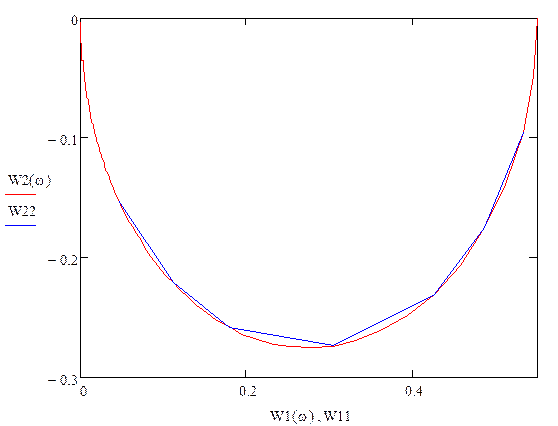
Найдем частоту, время окончания расчета, время гармонического анализа и шаг расчета:

·  Найдем :

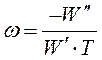
ω рад/с
9,99997914
19,9995436
30,00023484
49,99945152
80,00198701
109,9978132
184,9979485

Её мы указываем в генераторе гармонического сигнала.

·  Найдем частоту f:

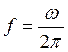
f Гц
1,59154611
3,18302622
4,77468567
7,95765986
12,73271169
17,50669569
29,44333797

Это основная частота.

·  Найдем Т, Т_гарм и Т_ок

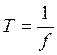, T_ок=7Т, Т_га=5Т,

T	Tok	Tra
0,62831984	4,39823889	3,14159921
0,31416643	2,19916504	1,57083217
0,20943787	1,4660651	1,04718935
0,12566508	0,87965559	0,62832542
0,07853787	0,54976506	0,39268933
0,057121	0,39984701	0,28560501
0,03396354	0,23774478	0,1698177

Т_гарм ­– время разложения

T_ок – схемное время окончания расчета, конец интервала и момент завершения осциллографирования.

·  Найдем h

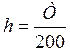
	h
	0,0031416
	0,00157083
	0,00104719
	0,00062833
	0,00039269
	0,00028561
	0,00016982

h – шаг интервала.

·  Модель:

где:

BLT 091 – генератор гармонического сигнала

BLT 133 – инерционное звено первого порядка

BLT 014 – осциллограф

BLT 015 – табулятор

На табуляторе и осциллографе заданы сигналы 101 и 201.

После серии расчетов получили следующие значения:

Xm	φ
0,54128	-0,178098
0,51743	-0,345546
0,48389	-0,495114
0,40876	-0,732827
0,31368	-0,963803
0,24793	-1,10309
0,15817	-1,27903

В вычислительном комплексе «РИТМ» были получены значения в полярной системе координат, преобразуем их в декартовые координаты, для построения экспериментальной кривой

                             

                         

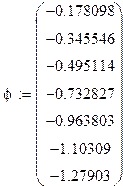
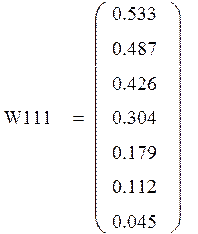
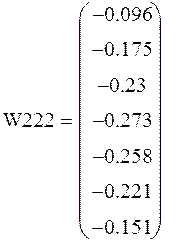
Полученная осциллограмма при

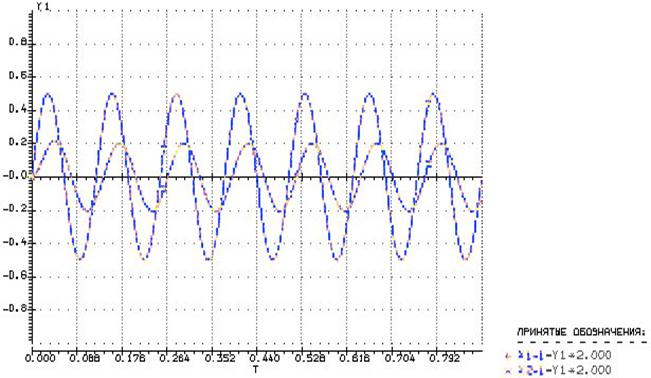
Наложим теоретическую кривую и полученные значения в программе “Ритм” и сравним её с кривой, полученной при трассировке:

Теоретическая и трассировка:

Теоретическая и экспериментальная:

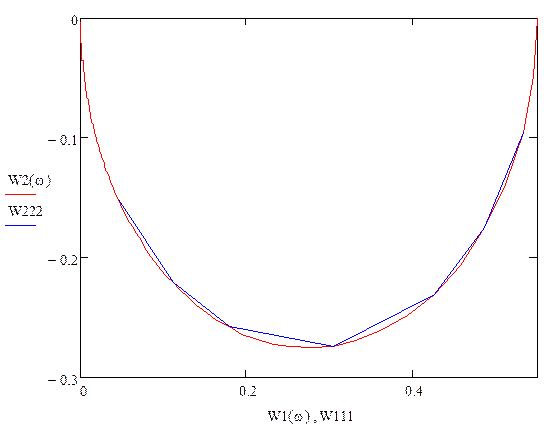
Трассировка и экспериментальная:

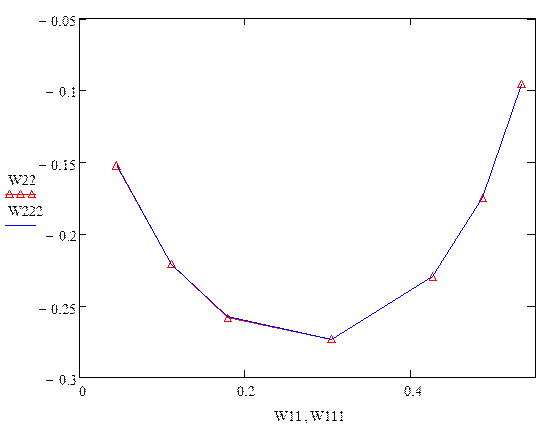
Как видно, точки, полученные экспериментально и трассировкой, совпали.