Уравнения Парка-Горева при исследовании электромагнитных переходных процессов в синхронной машине

Лекция 22

УРАВНЕНИЯ ПАРКА-ГОРЕВА ПРИ ИССЛЕДОВАНИИ ЭЛЕКТРОМАГНИТНЫХ ПЕРЕХОДНЫХ ПРОЦЕССОВ В СИНХРОННОЙ МАШИНЕ

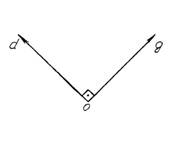
Уравнение Парка – Горева позволяет определить все параметры режима изменяющиеся во времени переходного процесса.

В системе уравнений 2 коэффициенты индуктивности и взаимоиндуктивности являются переменными и зависят от положения ротора в пространстве. Таким образом получаем систему диф. уравнений с переменными коэффициентами. Решением такой системы достаточно сложно, поэтому на практике переходят от отрезных координат к координатам d, q, o, то есть трехосную машину представляют в виде двуосной.

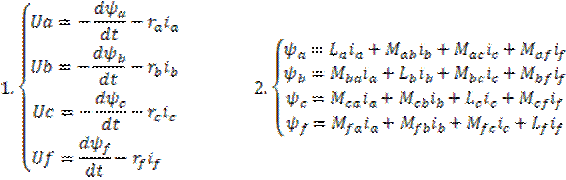
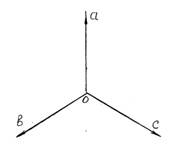
Переход к двуосной машине позволяет уменьшить число уравнений (отсутствие взаимоиндукции)           Для того, чтобы коэффициенты самоиндукции и взаимоиндукции не зависели от положения ротора в пространстве, будем считать, что оси d и q вращаются с синхронной скоростью в ту же сторону что и ротор.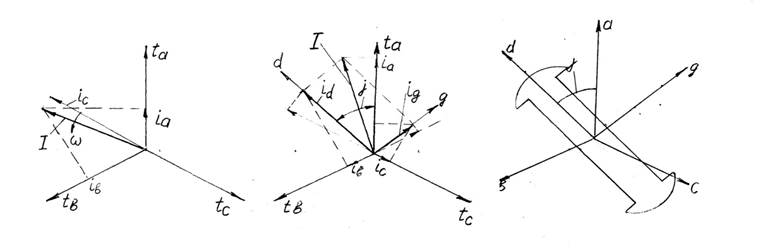

I – обобщенный вращающийся вектор.

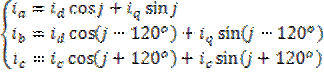
- Если система векторов является уравновешенной.

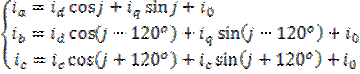
- Т. к.  во всех фазах одинакова, она не влияет на обобщенный вектор.

Переходим от фазных величин к величинам в осях d и q

 – угол между полем мотора в координатах d, q и фазной осью а.

Применяя систему координат d и q и изображая все величины систему в виде двух составляющих соответственно по осям d и q, векторы  и e в каждый момент.

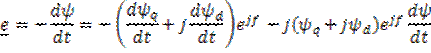
Отсюда

Для получения уравнений нагруженной машины вычитаем из составляющих ЭДС   и   падения напряжения, созданные токами  и  в сопротивлениях рассеяния и активном сопротивлении статора генератора. Падение напряжения в сопротивлениях рассеяния учтено в потокосцеплений  и .

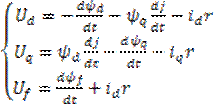               Уравнение Парка – Горева.

 и  – составляющие напряжения на шинах.

Данные уравнения применяются при уточненных расчетов переходных процессов в электрических системах. Каждый член системы уравнений связан с физикой процессов, происходящих в машине.

  и    – ЭДС, обусловленные перемещением в пространстве потокосцеплений  и  (ЭДС – вращения).

  – обусловленные перемещением потокосцеплений в пространстве с синхронной скоростью и дополнительные , , проявляющиеся в переходном процессе, когда угол δ отклоняется от установившегося значения.

 и  – трансформаторная ЭДС обусловленная пульсацией потокосцеплений  и  в течении переходных процессов.

Уравнения Парка – Горева дают связь между ЭДС, напряжением, токами, потокосцеплениями и параметрами рассматриваемой системы.           Если напряжение U не зависит от режима системы (шины неизменного напряжения), то уравнение полностью характеризует переходной процесс.           Если это напряжение не зависит от  режима системы, то необходимо составить дополнительные уравнения, выделяющих эту зависимость.           Если к уравнениям:

добавить уравнение момента, которое равно , то с помощью уравнения Парка – Горева можно исследовать электромеханические переходные процессы.