несимметрии. Между этими точками и приложено падение напряжения ΔU1 – в схеме прямой последовательности. Схема замещения нулевой последовательности начинается от места, где возникла продольная несимметрия, при этом напряжение нулевой последовательности прикладывается не по отношению к земле, а в рассечку проводов где возникла несимметрия. Все три провода с обеих сторон соединяются накоротко. Циркуляция токов нулевой последовательности возможна только в том случае, если имеются заземляющие нейтрали с обеих сторон от места продольной несимметрии или в том случае, если имеются обходные пути, по которым может замыкаться ток нулевой последовательности.
Имеются принципиальные различия в преобразовании схем и получении суммарного сопротивления при поперечной и продольной несимметрии. Чтобы понять их рассмотрим пример.
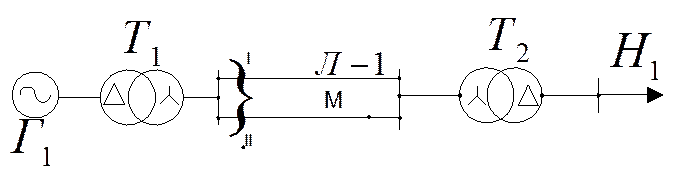
|
Поперечная несимметрия.
Чтобы получить Х1Σ:
|
Продольная несимметрия. В точке М разрыв.
U1 включается в то место, где возникла продольная несимметрия.
Э. д. с. Имеют сдвиг по фазе.
|
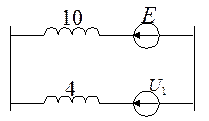
![]()
В схеме обратной последовательности Е = 0; остальное все так же.
Составим схему замещения нулевой последовательности.
|
|
Во
II цепи и I цепи разные условия. Между
ними взаимоиндукция. Чтобы ее учесть, необходимо составить схему замещения с
элементарными связями. С одной стороны эти цепи в одинаковых условиях, а с
другой – нет.
|
1. Разрыв одной фазы.
![]()
![]()
![]() İLA ΔÚLA
Особая фаза А
İLA ΔÚLA
Особая фаза А
![]()
![]()
![]()
![]() İLB
İLB
![]()
![]()
![]()
![]() İLA
İLA
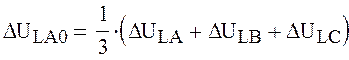 İLA
= 0 (4)
İLA
= 0 (4)
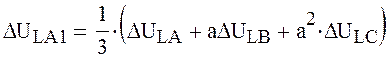
ΔÚLВ = 0 (5)
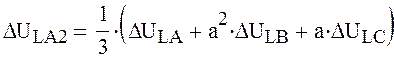
ΔÚLС = 0 (6)
Используя (5) и (6) получим:
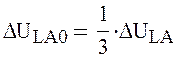 |
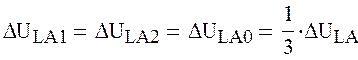
;
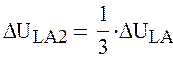
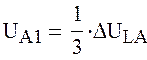 |
;
Полная аналогия для симметричных составляющих при двухфазных к.з. на землю.
Используя (4) получили:
![]()
![]()
![]() (2) и
(3):
(2) и
(3):
+ХL2Σ·ILA0
![]() +ХL0Σ·ILA2
+ХL0Σ·ILA2
ХL2Σ (ILA2 + ILA0) = ILA0 (ХL2Σ + ХL0Σ)
– ILA1
|
ILA2 (XL2Σ + XL0Σ) = XL0Σ (İLA2 + İLA0)
– ILA1
|
(*)
Используя (1):
–jXL2Σ ·ILA2 = EΣ – jXL1Σ·İLA1
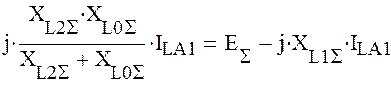
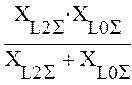
|
XΔL(1) =
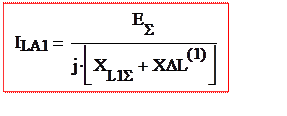
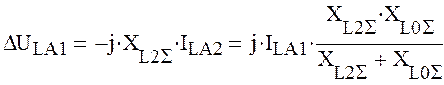
|
Фактически необходимо рассчитать ток прямой последовательности.
При суммировании симметричных составляющих достаточно графического суммирования.
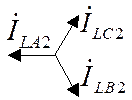
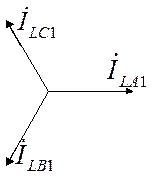
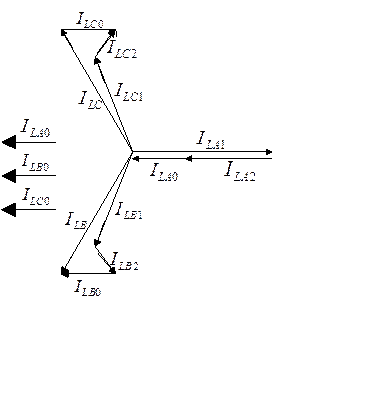
2. Разрыв двух фаз.
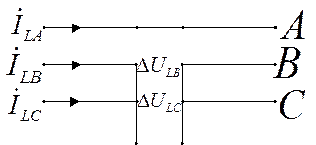
Дополнительные условия:
![]() (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
Выражение для симметричных составляющих тока:
![]()
![]()
![]()
![]() аналогия с однофазным
к.з.
аналогия с однофазным
к.з.
Воспользуемся (1) + (2) + (3)
![]()
![]()
![]()
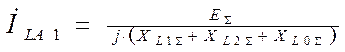
|
![]()
![]()
![]()
Достаточно
графического суммирования. 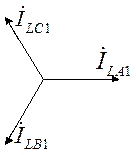
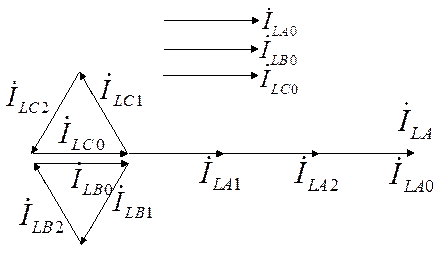
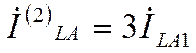
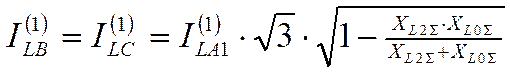
Комплексные схемы замещения.
Полученные соотношения позволяют произвести соединение схем отдельных последовательностей для получения так называемых комплексных схем замещения.
1. Разрыв одной фазы.
![]()
![]()
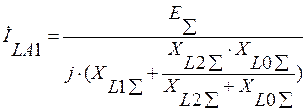
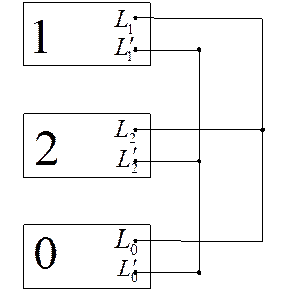
2. Разрыв двух фаз.
![]()
![]()
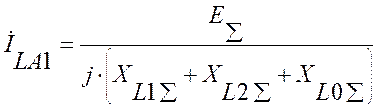
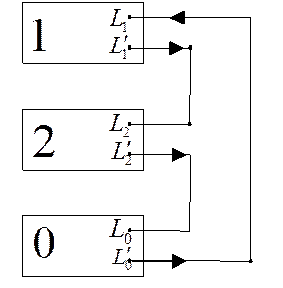
Комплексные схемы замещения используются также на расчетных столах. При поперечной несимметрии комплексные схемы другие, а все остальное рассчитывается так же.
Применение принципа наложения.
Случай, когда схема сложная и соединяет несколько источников питания, очень сложно определить ЕΣ, т.к. необходимо учитывать сдвиг по фазе между ними. Поэтому в случае в случае расчета неполного режима удобно применять принцип, если известен предшествующий режим (I,U). Это номинальные I,U. В этом случае неполный режим можно представить как результат наложения предшествующего режима на собственно аварийный, который определяется из условия, что в схеме в месте разрыва прямой последовательности включен источник тока - I0LA (“0” означает предшествующий режим). Если наложить эти режимы, то получим что в месте разрыва I0LA = 0 (+I0LA, - I0LA). Для вычисления I,U после разрыва достаточно рассчитать только собственно аварийный режим (это легко, т.к. имеется один источник). Затем необходимо произвести наложение. Т.к. в предшествующем режиме токи обратной и нулевой последовательности отсутствовали, то токи обратной и нулевой последовательности собственно аварийного режима являются полными токами обратной и нулевой последовательности. А полный ток прямой последовательности равен сумме токов прямой последовательности ___ и тока предшествующего режима. Токи ___ это чисто индуктивные токи, а прямой – не являются чисто индуктивными. Однако при суммировании этими факторами обычно пренебрегают, т.е. суммируют арифметически. Погрешность не существенна, а расчет прост.
Комплексная схема замещения для собственно аварийного режима.
1. Разрыв одной фазы.
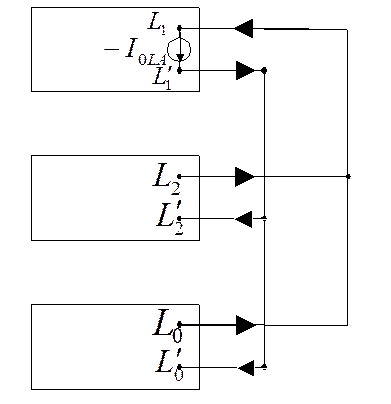
Для ___ источник включен в место разрыва, поэтому схемы соединены параллельно. Это источник тока, он единственный. Токи распространяются обратнопропорциональными величинами сопротивлениями.

Положительное направление тока – это направление тока предшествующего режима.
2. Разрыв двух фаз.
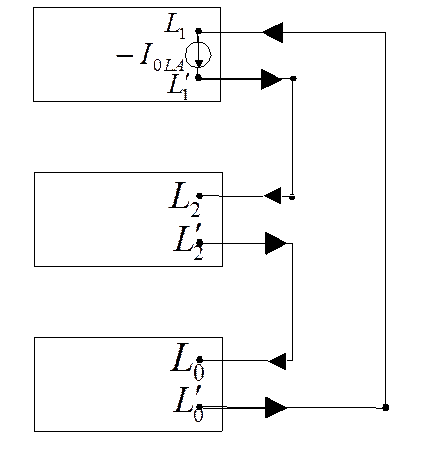
В случае разрыва двух фаз: 0 и Н последовательно и параллельно к схеме прямой последовательности.
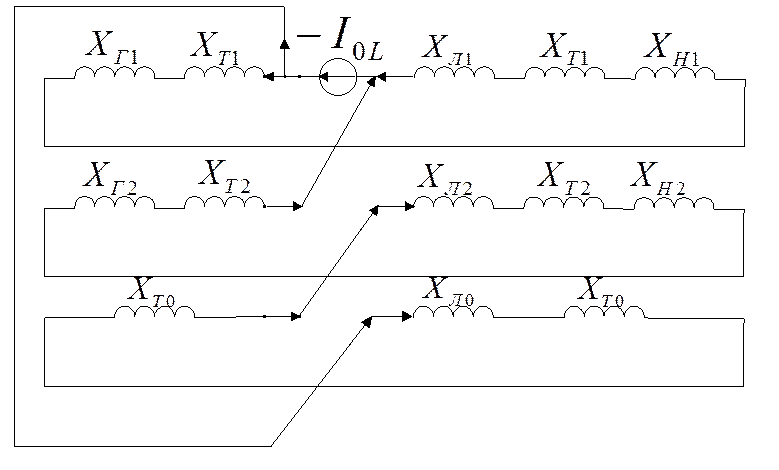
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.