Модель синхронного генератора в фазных координатах

Содержание

Введение.

1.  Математическое описание СГ.

1.1 Исходные уравнения.

1.2 Индуктивности обмоток синхронной машины.

2. Общие сведения.

2.1 Simulink.

2.2 Библиотека Simulink.

3. Создание модели СГ.

3.1 Создание математической модели.

3.2 Создание подсистем.

3.3 Холостой ход синхронного генератора, включение на активно-индуктивную нагрузку.

4. Ошибки.

Выводы.

Список литературы.

Проектирование и анализ систем автоматического управления в настоящее время немыслимы без применения средств вычислительной техники. К последним относится хорошо зарекомендовавшая себя система инженерных и научных расчетов Matlab и система моделирования динамических и событийно-управляемых систем – Simulink.

Пакет Matlab 6.5 выполнен, как математическое дополнение, в котором возможно реализовать все существующие функции. Это современный пакет мирового уровня, позволяющий быстро, качественно получить искомый результат.

Matlab включает в себя следующие инструментальные средства:

- библиотека сбора данных;

- набор анализа и исследования;

- визуализация процессов;

- прототип алгоритма и его развитие;

- моделирование и симуляция;

- программирование и использование разработок.

Система Simulink является расширением системы инженерных и научных расчетов Matlab и позволяет решать задачи такие как: сокращение времени проектирования, повышение качества разработки моделей физических систем и моделирование процессов в этих системах.

Для визуализации и анализа областей устойчивости удобно использовать структурные схемы математической модели.

Для более глубокого ознакомления с данным пакетом рассмотрим модель синхронного генератора (далее - СГ). Рассмотрим схему моделирования СГ в фазных координатах A, B, C.

1.  Математические уравнения синхронного генератора

Для процесса моделирования необходимо математически описать моделируемую систему. Для этого составим все необходимые уравнения СГ в фазных координатах.

1.1.  Исходные уравнения

Принципиальная схема синхронной машины, ротор которой имеет явно выраженные полюсы, представлена на рисунке 1.1, где стрелками указаны принятые положительные направления токов и напряжений в обмотках статора и ротора. Соответственно этому, когда ток в обмотке статора или ротора положителен, создаваемый им магнитный поток также считается положительным. Положительные направления магнитных осей фазных обмоток статора (А, В, С) и магнитных осей ротора (d, q) на рисунке 1.1 также отмечены стрелками.

Дифференциальные уравнения равновесия э.д.с. и падений напряжений в каждой из обмоток будут:

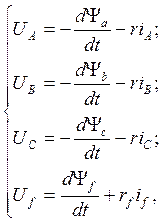                                                                           (1.1)

где     r и  — активные сопротивления соответственно контуров каждой фазы и цепи возбуждения;  и  — результирующие потокосцепления соответствующих обмоток (включая их потокосцепления рассеяния).

Раскроем выражения для потокосцеплений, которые при принятых допущениях представляют собой линейные зависимости от тока данного контура и токов магнитносвязанных с ним других контуров. Коэффициентами пропорциональности при этом будут индуктивность L рассматриваемого контура и его взаимоиндуктивности М с другими контурами. Введя у L и М индексы соответствующих обмоток, можно написать:

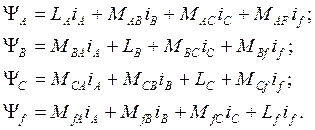                            (1.1)

Число различных значений М в действительности в 2 раза меньше, так как по принципу взаимности М_АВ = - М_BA, M_Bf = M_fB и т. д.

Если бы все L и М оставались неизменными, то система (1.1) состояла бы из линейных дифференциальных уравнений с постоянными коэффициентами, и решение её не представляло бы принципиальных