Исследование динамической устойчивости простейшей нерегулируемой электрической системы (Лабораторная работа № 4)

Лабораторная работа №4

Исследование динамической устойчивости простейшей нерегулируемой электрической системы

Цель работы:

1. Определение характера изменения угла сдвига вектора ЭДС и напряжения приемной системы (), скорости вращения ротора генератора () и активной мощности генератора () в простейшей нерегулируемой электрической системе при отключении одной из цепей высоковольтной линии электропередач (ЛЭП) в зависимости от длины отключаемой линии и ее активного сопротивления.

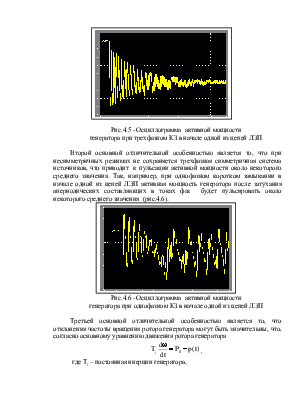
2. Определение характера изменения тех же параметров при  коротком замыкании (КЗ) в начале одной из цепей ЛЭП в зависимости от вида КЗ, и его длительности.

Указания по подготовке к работе:

1. Изучить теорию переходных процессов в простейшей нерегулируемой электрической системе при отключении одной из цепей высоковольтной линии электропередач и различных видах КЗ.

Рекомендуемая литература [       ]

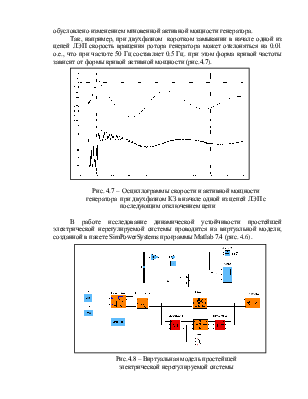
2. Ознакомиться с виртуальной моделью  для исследования динамической устойчивости простейшей нерегулируемой электрической системы, созданной в пакете SimPowerSystem программы Matlab 7.4.

Краткие пояснения к работе

В работе исследуется динамическая устойчивость простейшей нерегулируемой электрической системы (рис.4.1, а), а именно способность системы возвращаться в исходное состояние или близкое к исходному при больших возмущениях. За большие возмущения принято отключение одной из цепей ЛЭП или КЗ в начале одной из цепей ЛЭП (рис.4.1 б, в).

При любых возмущениях в системе нарушается баланс между мощностью турбины Р_Т и  активной мощностью выдаваемой  генератором Р, что приводит к изменению скорости вращения ротора генератора w. Возмущения могут быть настолько сильными, что генератор может выпасть из синхронизма. С целью выработки мероприятий по предотвращению нарушения устойчивости необходимо исследовать электромеханические переходные процессы, которые при этом возникают. Наиболее информативными параметрами при исследовании электромеханических переходных процессов являются активная мощность выдаваемая генератором Р и  угол d, которые при синхронной работе генератора с системой остаются постоянными.

 

Рис.4.1- Расчетная схема электрической системы:

а) исходный режим;  б) отключение одной цепи ЛЭП; в) КЗ в начале одной из цепей ЛЭП

Схема замещения электрической системы для исходного режима имеет вид (рис.4.2)

Рис.4.2 – Схема замещения электрической системы

При исследовании устойчивости электрической системы  расчетным путем используют метод площадей с построением угловых характеристик мощности (рис. 4.3)

Рис.4.3 – Угловые характеристики активной мощности

Математические выражения для статических угловых характеристик активной мощности для различных режимов имеют вид (при условии пренебрежения активными сопротивлениями элементов системы):

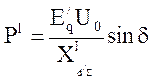 - Угловая характеристика мощности исходного режима;

 - Угловая характеристика мощности   послеаварийного режима (при отключении одной  цепи ЛЭП);

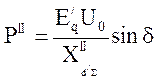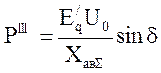- Угловая характеристика мощности аварийного режима (при КЗ в начале одной из цепей ЛЭП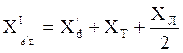), 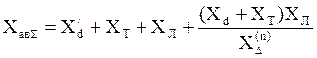где , ,  

, где - сопротивление шунта, зависящее вида КЗ

При отключении, например, одной из цепей ЛЭП  активная мощность генератора Р становится меньше мощности турбины Р_т  и ротор генератора начинает ускоряться. В период ускорения  ротор  запасает кинетическую энергию, которая математически выражается как интеграл 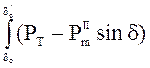 и представляется графически в виде площадки  1-2-3-1 (площадка ускорения А_уск).  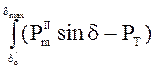В период торможения при Р>Р_т  ротор возвращает эту запасенную кинетическую энергию, которая выражается как интеграл  и представляется графически в виде площадки 3-4-6-3 (площадка торможения А_торм). Площадка 3-4-5-6-3 представляет собой площадку возможного торможения А_{возм.торм}. (рис.4.4)

 

Рис. 4.4 - Угловые характеристики активной мощности

Согласно методу площадей система будет динамически устойчива, если площадка ускорения будет не больше площадки возможного торможения.

Отношение возможной площадки торможения к площадке ускорения называется коэффициентом запаса динамической устойчивости

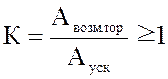   - практический критерий динамической устойчивости.

Точная оценка динамической устойчивости при учете всех видов переходных процессов и изменений в системе весьма сложна, поэтому исследование расчетным путем основывается на ряде допущений:

1.  Вращающий момент в переходном процессе не меняется.

2.  Замена совокупности генераторов одним эквивалентным;

3.  Малость отклонений частоты вращения ротора генератора от синхронной;

4.  Рассмотрение переходных процессов на ограниченном интервале времени;

5.  Сохранение трехфазной системы источников при ее нарушении в электрической сети. Несимметричные КЗ рассматриваются как симметричные, удаленные на соответствующий аварийный шунт;

6.  Не учитывается нелинейность параметров системы;

7.  При изменении режима мгновенно изменяется электрическая мощность;

8.  Расчеты ведутся исходя из неизменности результирующего потокосцепления обмотки возбуждения в продольной оси во время всего переходного процесса, т.е исходя из постоянства ЭДС E^/_q. В упрощенных расчетах E^/_q обычно приближенно принимается ЭДС равной Е^/.

Более полную картину протекания электромеханического переходного процесса дает компьютерная модель электрической системы, что позволяет получить изменение мгновенных значений угла сдвига вектора ЭДС и напряжения приемной системы, скорости вращения ротора генератора и активной мощности во времени. В таком случае число допущений сокращается (остаются первые два), что приводит к несколько иной картине протекания электромеханического переходного процесса.