Противогоночное кодирование автоматов, страница 2

Сокращённая таблица пар переходов, подлежащих развязыванию:

№	(по )	(по )	(по )	(по )
1	(12),(34)	(11),(40)	(06),(12)	(01),(23)
2	(12),(50)	(23),( 40)	(06),(34)	(01),(45)
3	(12),(78)	(23),(50)	(06),(78)	(01),(67)
4	(12),(90)	(23),(67)	(06),( 95)	(01),(89)
5	(34),(50)	(23),(89)	(12),( 95)	(23),(45)
6	(34),(78)	(40),(67)	(34),( 95)	(45),(67)
7	(34),(90)	(40),(89)	(78),( 95)	(45),(89)
8	(50),(78)	(50),(67)
9	(66),(90)	(50),(89)
10	(78),(90)	(67),(89)

Противогоночное кодирование:

                                   

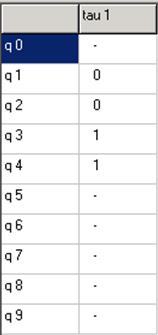
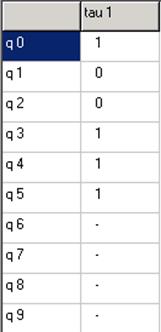
Переходы (12),(34) развязаны.        Переходы (12),(50) развязаны.

                               

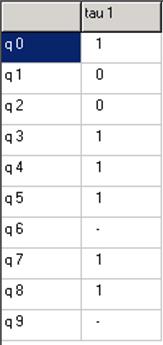
Переходы (12),(78) развязаны.        Переходы (12),(90) развязаны.

Добавляем разряд

          

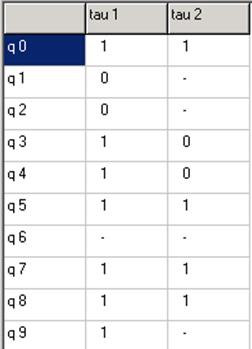
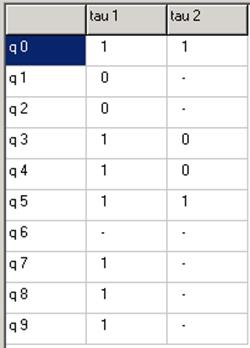
Переходы (34),(50) развязаны.                 Переходы (34),(78) развязаны.

Переходы (34),(90) развязаны.

Добавляем разряд

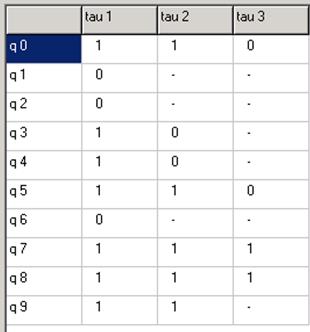
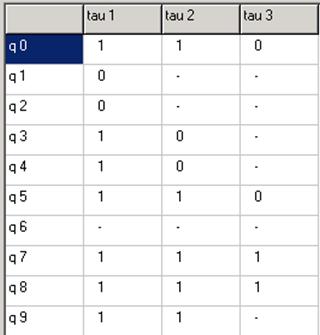
Переходы (50),(78) развязаны.                        Переходы (66),(90) развязаны.

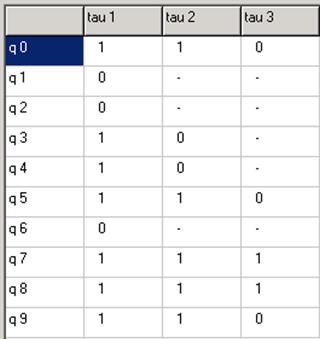
Переходы (78),(90) развязаны.

Развязаны все переходы в M0.

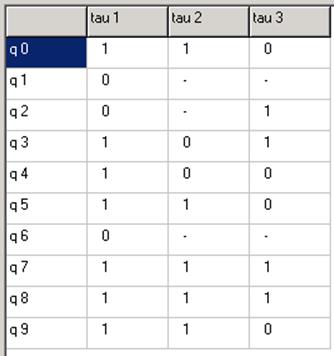
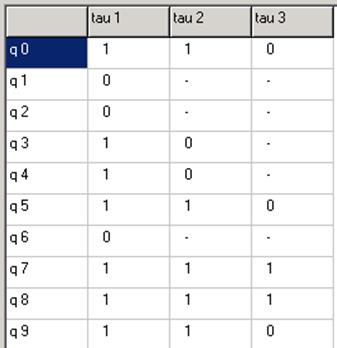
Переходы (11),(40) развязаны.                          Переходы (23),(40) развязаны.

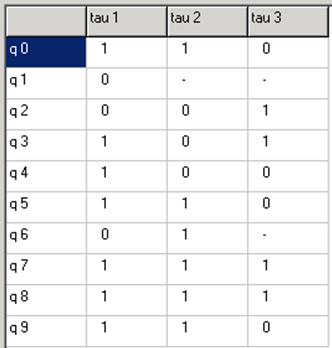
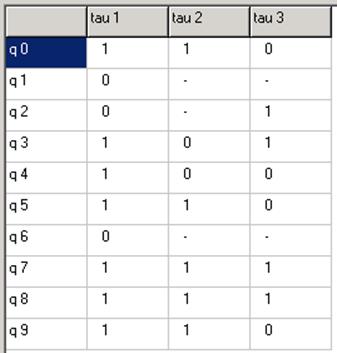
Переходы (23),(50) развязаны.                        Переходы (23),(67) развязаны.

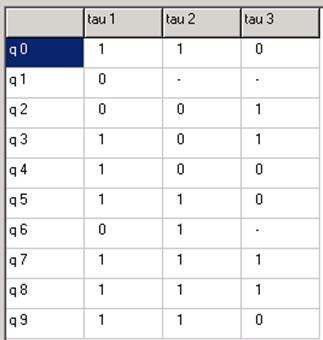
Переходы (23),(89) развязаны.                           Переходы (40),(67) развязаны.

Добавляем разряд .

Переходы (40),(89) развязаны.

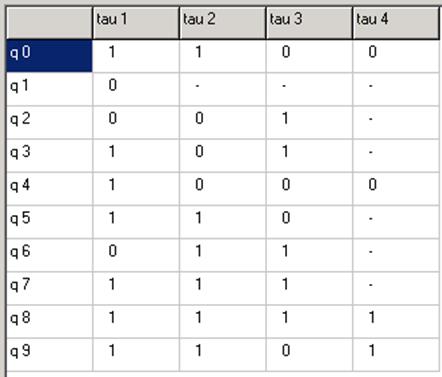
Переходы (50),(67) развязаны.

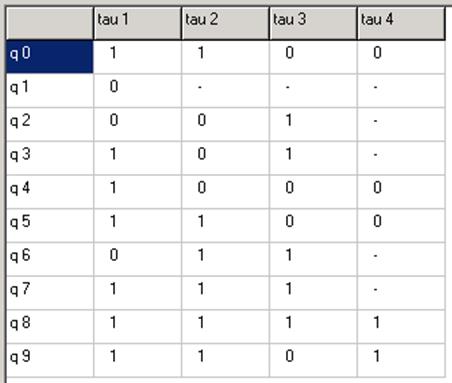
Переходы (50),(89) развязаны.

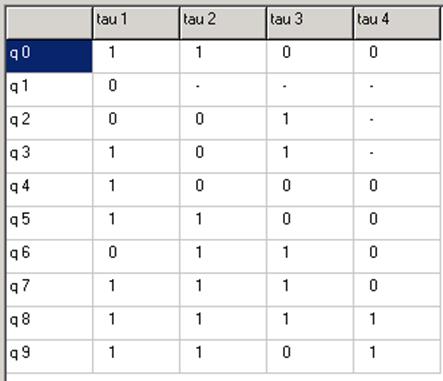
Переходы (67),(89) развязаны.

Развязаны все переходы в M1.

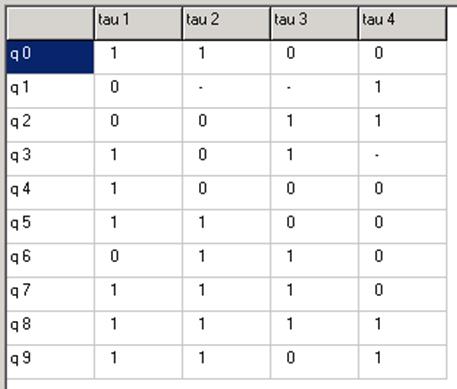
Переходы (06),(12) развязаны.

Переходы (06),(34) развязаны.

Добавляем разряд .

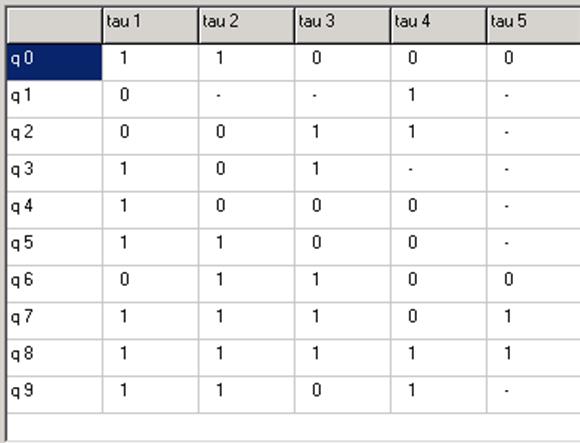
Переходы (06),(78) развязаны.

Переходы (06),(95) развязаны.

Переходы (12),(95) развязаны.

Переходы (34),(95) развязаны.

Переходы (78),(95) развязаны.

Развязаны все переходы в M2.

Переходы (01),(23) развязаны.

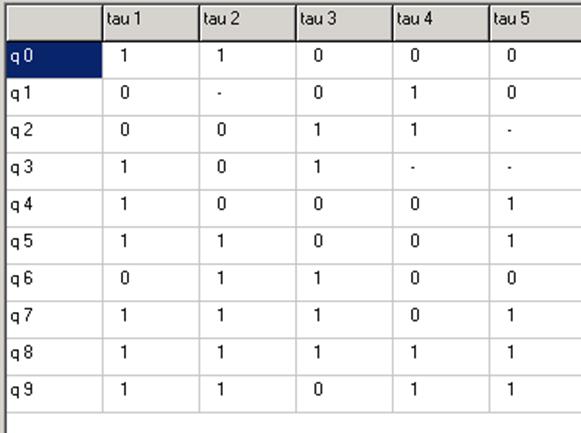
Переходы (01),(45) развязаны.

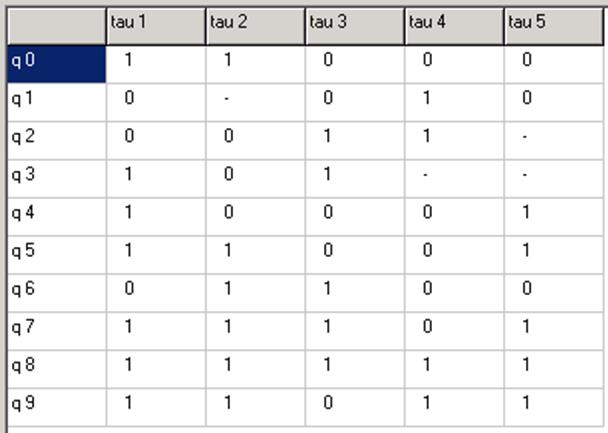
Переходы (01),(67) развязаны.

Переходы (01),(89) развязаны.

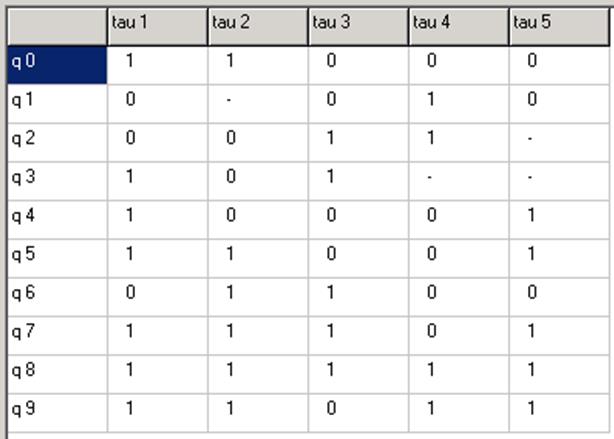
Переходы (23),(45) развязаны.

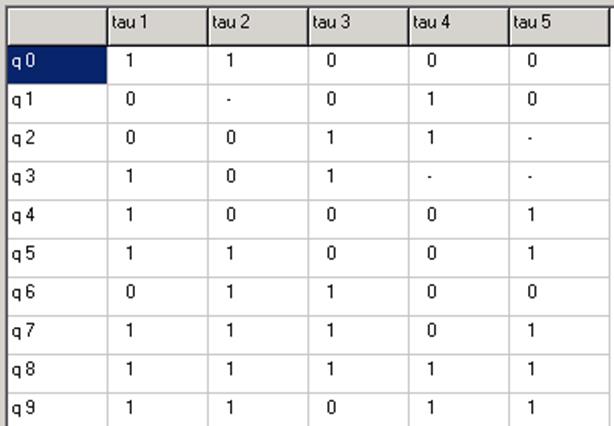
Переходы (45),(67) развязаны.

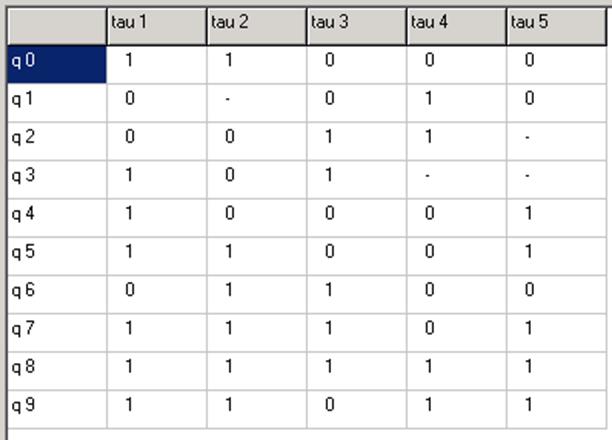
Переходы (45),(89) развязаны. Развязаны все переходы в M3. Получилось пять разрядов, а для кодирования десяти состояний достаточно четырёх. Минимизируем количество элементов памяти.

Исключим разряд . Получим следующую таблицу:

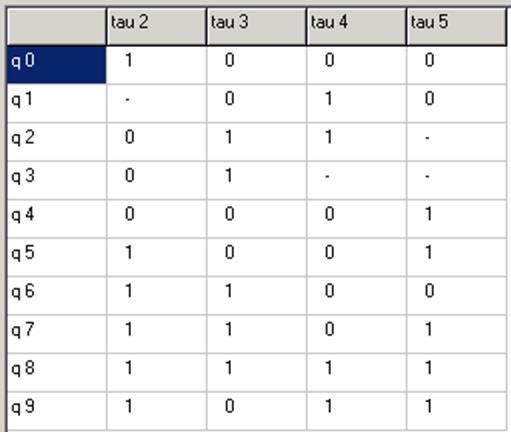
Повторим развязывание.

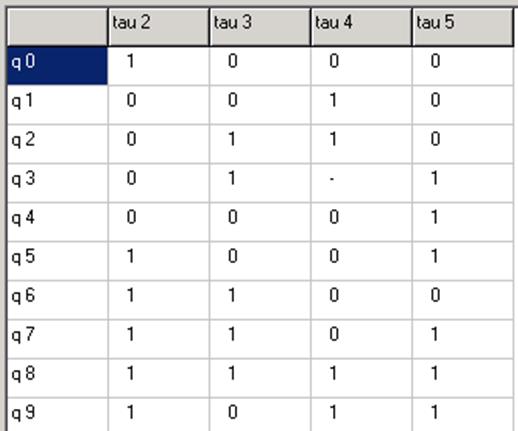
Получилось четыре элемента памяти. Дальнейшая минимизация невозможна.

Переименуем {, , , } в {, , ,  } и доопределим разряд . Получим следующую таблицу:

q
q0	1	0	0	0
q1	0	0	1	0
q2	0	1	1	0
q3	0	1	0	1
q4	0	0	0	1
q5	1	0	0	1
q6	1	1	0	0
q7	1	1	0	1
q8	1	1	1	1
q9	1	0	1	1

Получаем таблицы переходов и выходов автомата.

Таблица переходов:

X\q	1000	0010	0110	0101	0001	1001	1100	1101	1111	1011
00	1000	0110	0110	0001	0001	1000	1100	1111	1111	1000
01	1000	0010	0101	0101	1000	1000	1101	1101	1011	1011
10	1100	0110	0110	0001	0001	1001	1100	1111	1111	1001
11	0010	0010	0101	0101	1001	1001	1101	1101	1011	1011

Таблица выходов:

X\q	1000	0010	0110	0101	0001	1001	1100	1101	1111	1011
00	0	0	0	1	1	0	0	1	1	1
01	0	0	1	1	0	0	0	0	1	1
10	0	0	0	1	1	0	0	1	1	1
11	0	0	1	1	0	0	0	0	1	1