Наиболее помехоустойчивыми в отношении флюктуационных помех являются широкополосные виды модуляции (ЧМ, ФИМ, КИМ), т. е. такие, у которых спектр модулированного колебания значительно шире спектра модулирующей функции. Осуществляемое детектором свертывание широкополосного сигнала этих видов модуляции в узкополосный сопровождается суммированием сильно коррелированных спектральных составляющих сигнала и спектральных составляющих флюктуационной помехи, коррелированных тем слабей, чем шире полоса частот, в которой осуществляется суммирование при свертывании. В результате превышение сигнала над помехой Рс/Рш на выходе детектора тем больше, чем шире спектр модулированного колебания во сравнению со спектром модулирующей функции. Этот выигрыш может быть весьма значительным и достигается не в результате увеличения мощности сигнала или его длительности (как в методе накопления, а лишь за счет расширения спектра сигнала.
Оценка этого выигрыша получается из сравнения превышений сигнала над помехой на выходах широкополосного (ЧМ) и узкополосного (AM) приемников при одинаковых превышениях на их входах. Сравнение ЧМ с AM дает:
(Рс/Рш)ЧМ » 3,3b2(Рс/Рш)АМ, (2)
где b - максимальный индекс частотной модуляции, т.е. индекс, соответствующий наибольшему частотному отклонению. Например, в ЧМ-радиовещании принята девиация частоты Df = 75 кГц приширине спектра модулирующего сигнала DF = 5 кГц. При этом b = 15 и
(Рс/Рш)ЧМ » 700 (Рс/Рш)АМ, т.е. применение частотной модуляции, эквивалентно увеличению мощности сигнала на несколько порядков. Выигрыш получается тем больший, чем шире спектр ЧМ-сигнала.
Нужно, однако, иметь в виду, что указанные преимущества в помехоустойчивости широкополосных видов модуляции проявляются лишь при сравнительно небольших помехах (при Рс/Рш ³ 1).
Использование оптимальной фильтрации. Если на вход линейного фильтра поступает смесь сигнала и помехи x(t)=s(t)+x(t), то уместно поставить вопрос о том, как наилучшим образом выделить сигнал из этой смеси. Известными считаются статистические характеристики (спектр и корреляционная функция) случайных процессов, представляющих сигнал и помеху. Искомой является передаточная функция (частотные характеристики) оптимального фильтра. Оптимальный фильтр в равной мере ослабляет одинаковые спектральные составляющие принимаемого сигнала и помехи и подавляет спектральные составляющие помехи на тех частотах, где сигнал отсутствует.
Реализация корреляционного приема. Корреляционный приемник содержит устройства перемножения и усреднения (интегратор) и предназначен для образования на выходе функции корреляции смеси x(t)=s(t)+x(t) сигнала и помехи, поступающих на его вход.
Если все образцы сигнала известны на приемной стороне, то приемник может образовать функцию взаимной корреляции между принятой смесью x(t) и каждым образцом сигнала s(t)
.
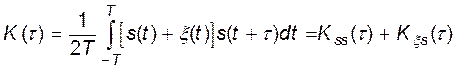где Т - достаточно большой интервал усреднения.
Если сигнал и помеха некоррелированы
или слабо коррелированы, то 
и напряжение,
пропорциональное 
, на выходе приемника
свидетельствует о наличии сигнала в смеси x(t).
При недостатке априорных сведений о сигнале можно воспользоваться тем, что радиосигналы, в отличие от флюктуационной помехи, хотя и не являются периодическими фациями времени, часто носят значительные черты периодичности. Для использования этого отличия сигнала от помехи в приемнике образуется автокорреляционная функция принятой смеси x(t)):
.
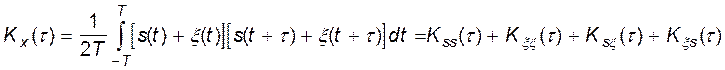При слабой корреляции между сигналом и помехой последние два слагаемых малы, первое является периодическим (как и сигнал), а второе практически равно нулю, если задержка t выбрана большей, чем ширина tx автокорреляционной функции помехи (рис.1).
Т.о.
при достаточно больших задержке t и времени
Т усреднения напряжение, пропорциональное , на
выходе приемника свидетельствует о наличии сигнала в смеси x(t).
Этот способ борьбы с помехой тем эффективнее, чем ярче выражена периодичность сигнала. Следовательно, повышение помехоустойчивости достигается за счет избыточности сигнала по длительности
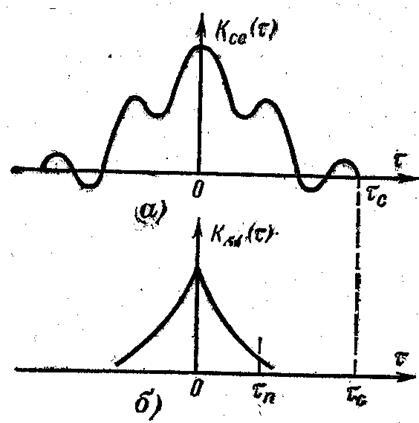
Рисунок 1 - Автокорреляционные функции сигнала (а) и помехи (б)
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.