Когерентные приемники дискретных сигналов

2.2.    Когерентные приемники дискретных сигналов

Литература:

1. Теория электрической связи: Учеб. /Под ред. Д.Д. Кловского. - М.: Радио и связь, 1999. - С.165-192.

Когерентный прием

Предположим, что все искажения в канале связи строго детерминированы и случайным является только аддитивный стационарный гауссовский белый шум n(t) с нулевым математическим ожиданием и спектральной плотностью N₀. Тогда принимаемая смесь одного из полезных сигналов и шума описывается уравнением

                                                                                                                        (1)

где все сигналы s_i(t) известны. Неизвестна лишь реализация помехи n(t) и номер (индекс i) действительно переданного сигнала, который и должно определить РУ.

Алгоритм работы оптимального приемника, анализирующего в этих условиях сигнал на интервале 0...Т_н, состоит в следующем.

Возьмем на интервале наблюдения  равноотстоящих отсчетов смеси x(t) с шагом . При отсутствии сигнала (гипотеза H₀) получаемые отсчеты независимы, поэтому их k-мерная плотность вероятности равна

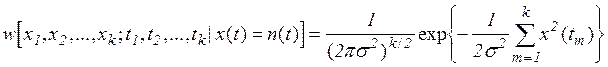,                                                                                                                        (2)

где - дисперсия (мощность) белого шума,

 - полоса анализируемых частот.

При гипотезе H_i о том, что передавалось сообщение l_i, согласно (1)  . Поскольку все сигналы s_i(t) известны, то условная k-мерная плотность вероятности отсчетов x(t) не изменится, если в формуле (2) значения  заменить разностью , представляющей при гипотезе H_i шум

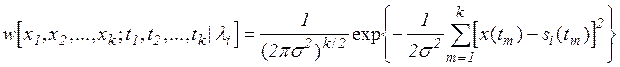.                                                                                                                        (3)

Соответственно, для всех М возможных сигналов определяются отношения правдоподобия (ОП) относительно нулевой гипотезы ()

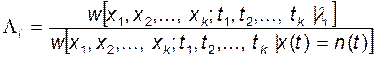                                                                                                                        (4)

или с учетом (2) и (3)

(5)

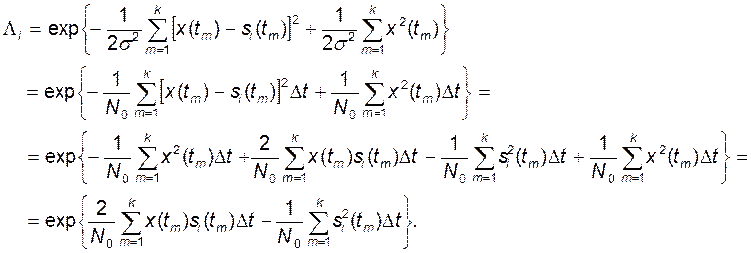
По правилу максимума правдоподобия в случае белого шума РУ должно выбирать значение i, обеспечивающее максимум ОП (4).

При расширении полосы  анализируемых частот число отсчетов  будет стремиться к бесконечности, а интервал между отсчетами  - к нулю. Суммы в (5) при этом обращаются в интегралы, а правило решения (оценки сообщения l_i) можно записать в следующем виде

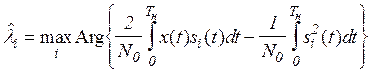.                                                                                                                       (6).

В (6) порядок вычисления функций max и Arg можно поменять местами

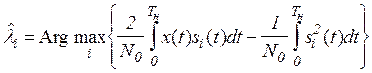.                                                                                                                        (7)

В оптимальных приемниках одной из важнейших составных частей является устройство, максимизирующее на выходе энергетическое отношение сигнал/шум (ОСШ). Подобные устройства реализуются либо по схеме коррелятора, либо в виде согласованного фильтра.

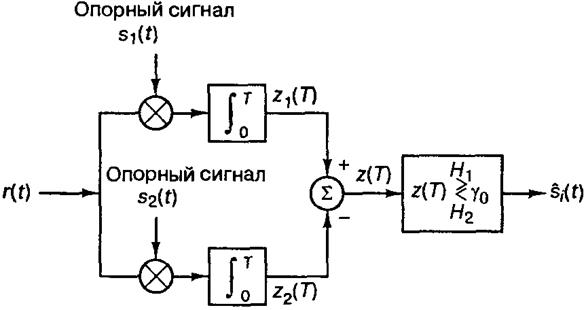
Корреляционный приемник

Содержит устройства перемножения и усреднения (интеграторы) и предназначен для образования на выходе корреляционной функции между принятой смесью x(t) и каждым из М возможных образцов сигнала s(t)

.

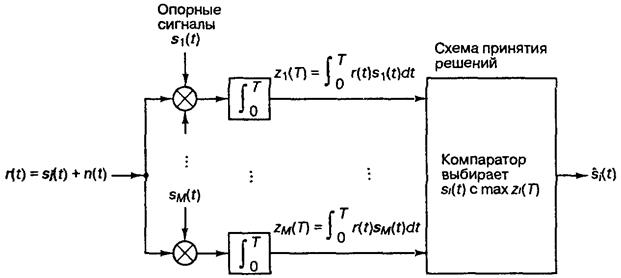
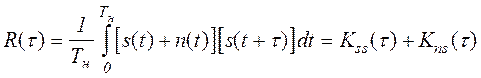Если сигнал и помеха некоррелированы или слабо коррелированы, то  и напряжение, пропорциональное , свидетельствует о наличии полезного сигнала в смеси x(t).

В радиосвязи ПРМ и ПРД разнесены в пространстве, что усложняет проблему создания когерентного опорного  напряжения. Если сигналы ПРД хорошо стабилизированы по частоте, то в ПРМ также можно применить высокостабильный генератор, периодически синхронизируемый колебаниями ПРД. Если же стабильность частоты ПРД невелика, то для создания опорного напряжения используется специальный канал синхронизации, представляющий собой систему ФАПЧ местного гетеродина ПРМ по принимаемым сигналам.

При обработке двоично-модулированных сигналов когерентный приемник может быть построен по одной из двух схем.

Первый вариант (двухканальный)

Второй вариант (одноканальный)

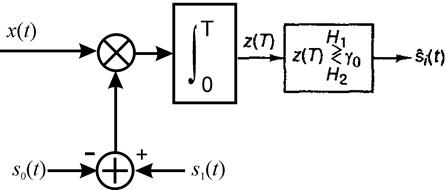
Корреляторы удобно использовать тогда, когда время Т_н наблюдения достаточно велико. Согласованные фильтры в основном используются при относительно малом времени наблюдения.

Приемник на основе согласованных фильтров

Если  - детерминированный сигнал, принимаемый на фоне аддитивного белого шума, то согласованным фильтром, обеспечивающим получение на выходе максимального ОСШ, является фильтр с импульсной характеристикой вида

, где  фиксированный промежуток времени.

Для физической реализуемости такого фильтра необходимо и достаточно, чтобы

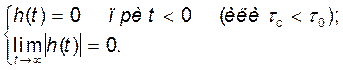
Из первого условия следует, что применение согласованных фильтров возможно только для сигналов ограниченной длительности.

Выполнение условий физической реализуемости согласованных фильтров не означает возможности их практического создания, т.к. технические трудности (сложность схемы, использование элементов с трудно выполнимыми характеристиками и др.) могут оказаться непреодолимыми.

Сигнал на выходе согласованного фильтра с точностью до постоянного множителя совпадает с автокорреляционной функцией (АКФ) входного сигнала

.

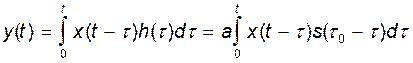Обозначим . Тогда

.

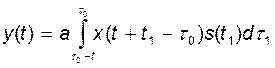В момент окончания полезного сигнала

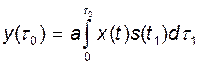 - КФ полезного сигнала и входной смеси.

Т.е. вид выходного сигнала согласованного фильтра значительно отличается от сигнала на входе.

Передаточная функция согласованного фильтра

, где   - функция, комплексно сопряженная со спектральной плотностью сигнала.

 - множитель, характеризующий временное запаздывание при прохождении сигнала через фильтр.

АЧХ согласованного фильтра определяется амплитудным спектром сигнала, а ФЧХ обратна по знаку фазовому спектру.

Благодаря этому в момент  все сильно коррелированные составляющие спектра принимаемого сигнала складываются в фазе (когерентно).

Оптимальный фильтр в равной мере пропускает одинаковые спектральные составляющие принимаемых сигнала и помехи и подавляет спектральные составляющие помехи на тех частотах, где сигнал отсутствует.