Синтез и исследование системы модального управления и наблюдателей Люенбергера

модифицированную систему модального управления с полными измерениями (по управляющему и возмущающему воздействиям);

з) модифицированную систему модального управления, замкнутую через наблюдатели полного и пониженного порядка (по управляющему воздействию с отклонением по НУ).

Исходные данные:

Вариант 36:

Структурная схема: № 12

Вариант параметров: № 1

Структурная схема САУ:

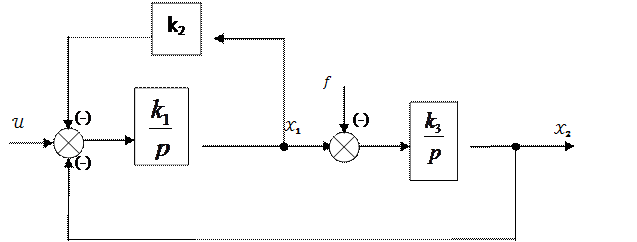Параметры элементов:

K₁ = 2.2

K₂ = 1.5

K₃ = 2

T₁ = 1

T₂ = 3

T₃ = 5

1. Представим математическое описание объекта управления , заданного структурной схемой, в виде дифференциальных уравнений в нормальной форме Коши.

Запишем уравнения для координат состояния  и .

Уравнения в операторной форме: 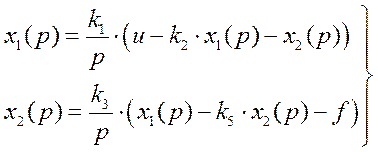  или

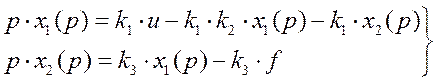
Переходя во временную область, получим математическую модель объекта управления в виде дифференциальных уравнений в нормальной форме Коши:

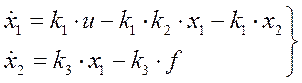
Векторно-матричную модель заданного объекта представим в форме:

                        

где x = [x₁, x₂]^T – двумерный вектор координат состояния, u, f – скалярные управляющее и возмущающее воздействия соответственно;

A – собственная матрица объекта управления

B –  матрица управлений

M – матрица возмущений

Составим матрицу объекта управления. Её строки соответствуют правым частям уравнений координат состояния, а столбцы – коэффициентам перед каждой координатой.

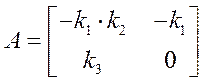
Матрица управлений представляет собой вектор-столбец, состоящий из коэффициентов перед управляющим воздействием. Если в каком-либо из уравнений нет, то коэффициент равен нулю.

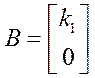
Аналогично составляется матрица возмущений:

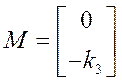
Подвергнем матричное уравнение (1) преобразованию Лапласа и выразим x:

где E - единичная матрица, по главной диагонали которой располагаются единицы, а все остальные элементы – нули. Разделив правую и левую части последнего выражения на u при f = 0, получим матричную передаточную функцию ОУ по управлению:

Аналогично при u = 0 получаем матричную передаточную функцию объекта управления по возмущающему воздействию:

Установившиеся значения координат состояния объекта при подаче единичного управляющего воздействия:

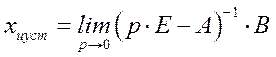
Установившееся значение при подаче единичного возмущающего воздействия:

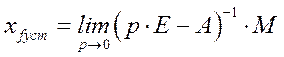
Здесь – обратная матрица, определяемая выражением

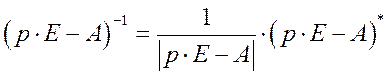
Характеристический полином ОУ зависит от собственной матрицы А и равен определителю

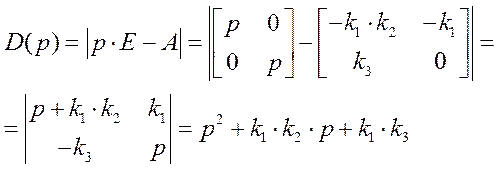
Получим присоединенную матрицу:

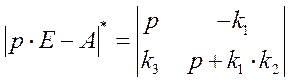
тогда

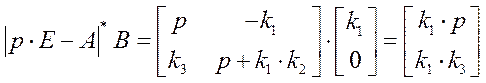
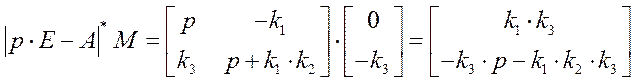
Установившиеся значения координат состояния при подаче единичного управления

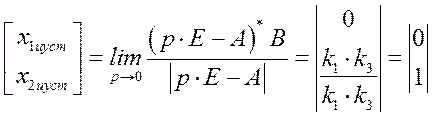
Установившиеся значения координат состояния при подаче единичного возмущения

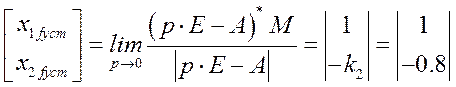
Произведём моделирование в системе Matlab Simulink и проверим расчёты.

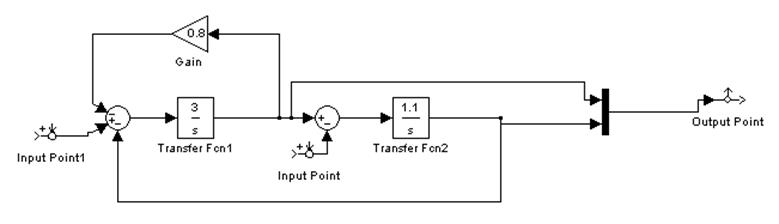
Рисунок 1. Моделирование единичного управляющего и возмущающего воздействия

	X2(t)
	X1(t)

 

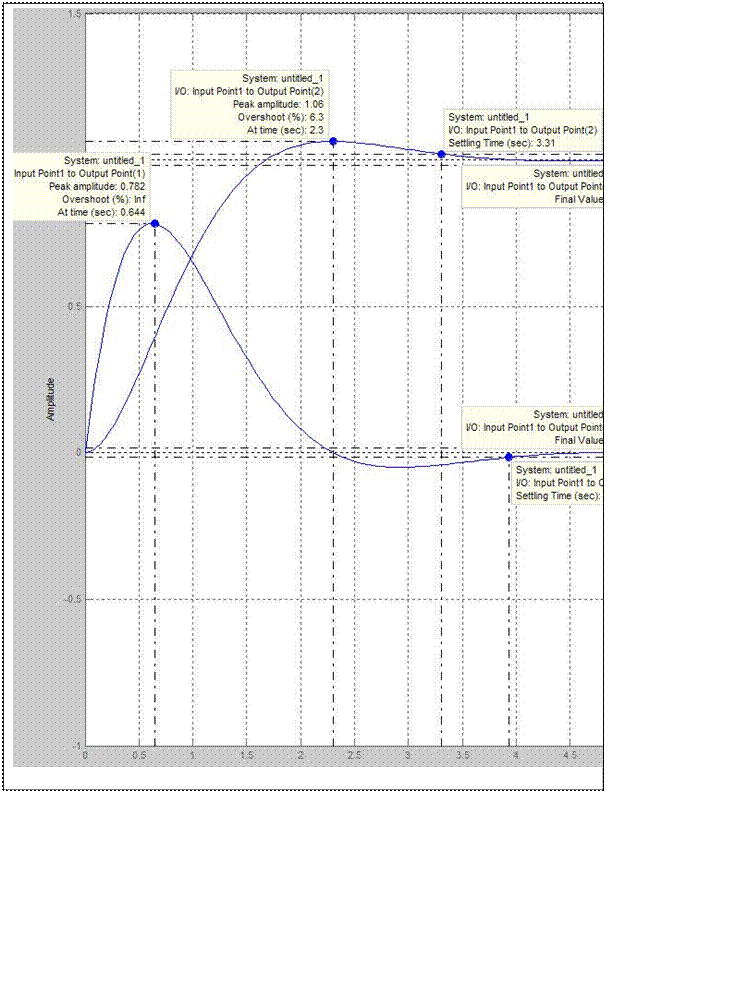
Рисунок 2. Моделирование установившихся значений координат состояния при подаче единичного управления

X2(t)

X1(t)

Рисунок 3. Моделирование установившихся значений координат состояния при подаче единичного возмущения

Переходные процессы в ОУ по управляющему воздействию изображены на рис.2.

Определим показатели качества по координате :

- установившееся значение:

- максимальное перерегулирование:

- время регулирования

- количество колебаний:

Определим показатели качества по координате :

- установившееся значение:

- максимальное перерегулирование:

- время регулирования

- количество колебаний:

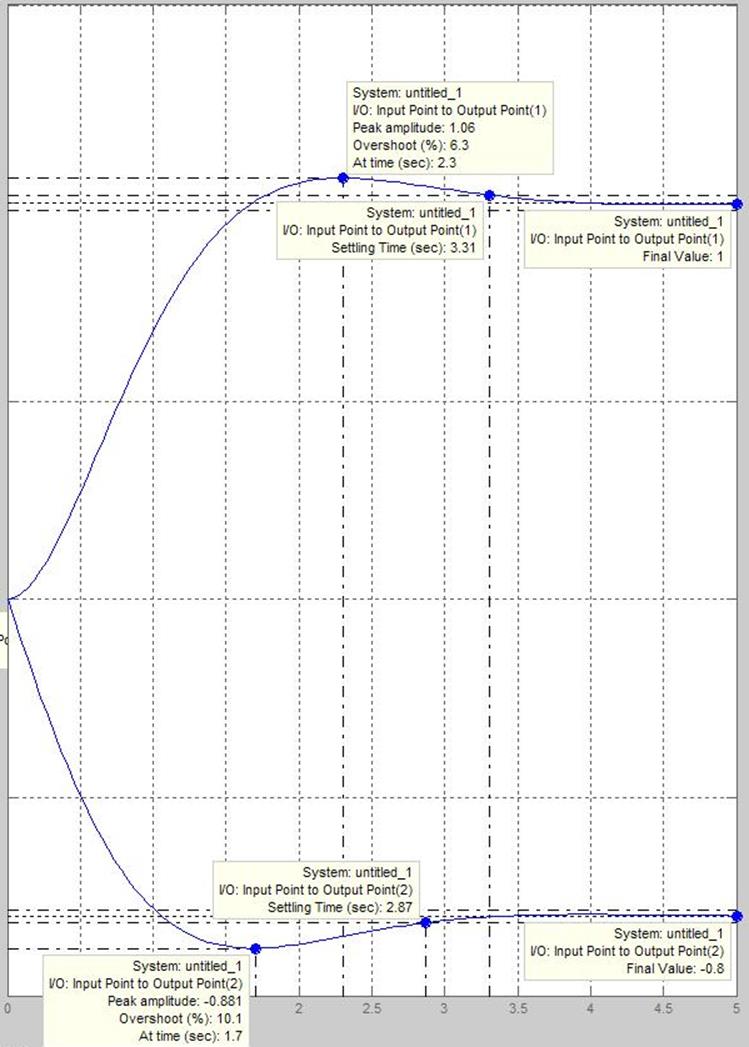
Переходные процессы в ОУ при возмущающем воздействии изображены на рис.3.

Определим показатели качества по координате :

- установившееся значение:

- максимальное перерегулирование:

- время регулирования

- количество колебаний:

Определим показатели качества по координате :

- установившееся значение:

- максимальное перерегулирование:

- время регулирования

- количество колебаний:

Вывод: Моделирование подтверждает теоретические расчёты. Сходимость результатов высокая.

2. Перед началом синтеза модального регулятора необходимо произвести проверку условия управляемости.

Для полной управляемости объекта необходимо и достаточно, чтобы матрица управляемости имела вид: , имела бы полный ранг (ранг матрицы управляемости равен порядку объекта) [1.7, с.8]:

rang(Y)=n.

Для заданного объекта матрица управляемости Y имеет вид

.

Найдем ранг матрицы Y:

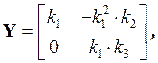
ее диагональный минор второго порядка равен

Из последнего неравенства следует, что рангY равен порядку объекта