Величины Вr – остаточная индукция и Нс – коэрцитивное поле характеризуют основные свойства ферромагнетика. Если значение Нс мало, т.е. петля узкая, то магнетик называют мягким, если значение Нс велико, то ферромагнетик называют жестким. Если значение Br высокое, то на основе таких ферромагнетиков возможно создание постоянных магнитов.
Отношение В/Н в каждой точке основной кривой намагничивания определяет тангенс угла наклона кривой в каждой точке и, в то же время, определяет значение магнитной проницаемости (рис.3).
Характерной особенностью кривой является наличие спонтанного намагничивания, т.е. в отсутствие внешнего магнитного поля в веществе возникают обменные силы, которые заставляют спины электронов в смежных атомах устанавливаться параллельно друг другу, образуя область спонтанного намагничивания, называемые доменами. (рис. 4.).
Домены в отсутствие магнитного поля ориентированны таким образом, что суммарный магнитный момент равен нулю. В магнитном поле наблюдается рост доменов, моменты которых составляют наименьший угол с направлением внешнего поля, за счет доменов, составляющих большие углы.
Далее наблюдается поворот магнитных моментов доменов в направление поля, при этом магнитные моменты электронов поворачиваются одновременно, оставаясь параллельными.
Данные процессы называются необратимыми, что и служит причиной гистерезиса.
Для каждого гистерезиса имеется определенная температура Тс называемая точкой Кюри, при которой ферромагнетик становится обычным парамагнетиком.
В некоторых веществах магнитные моменты электронов устанавливаются антипараллельно в пределах одного домена. Такие вещества носят название антиферромагнетиков.
ОПИСАНИЕ УСТАНОВКИ
На ферромагнитный образец намотаны симметрично две катушки, одна из которых L1 (первичная) имеет N1 витков и предназначена для создания магнитного поля в образце О.
Величина тока в первичной катушке регулируется с помощью потенциометра R и регистрируется микроамперметром. Вторичная обмотка L2 с числом витков N2 является регистрирующей. В измерительную цепь включен вольтметр.
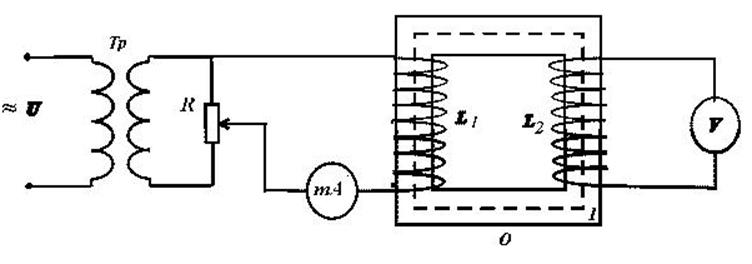Рис. 5.
О – исследуемый образец;
Тр – понижающий трансформатор.
Ток, протекающий в первичной катушке создает магнитное поле Н в ферромагнитном сердечнике. Величину этого поля можно оценить из соотношения:
,
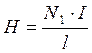(10)
Где Н – напряженность магнитного поля;
I – сила тока в катушке L1;
l – средняя длина образца;
N1
– число витков первичной катушки.
Сила тока в цепи первичной катушки изменяется по гармоническому закону, т.к. схема питается от сети переменного тока промышленной частоты
I = I0cos wt. (11)
Амперметр, включенный в
цепь первичной катушки, измеряет эффективное значение силы тока Iэфф, которое связано с амплитудным I0 следующим соотношением 
.
Переменное магнитное поле, возникающее в образце, создает, согласно закоу электромагнитной индукции, во вторичной катушке э.д.с., величина которой определяется соотношением:
,
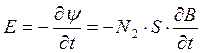(12)
Где y - потокосцепление;
N2 – число витков измерительной катушки;
В – магнитная индукция поля, возникающая в ферромагнитном образце.
Отсюда имеем:
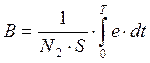(13)
Т.к. изменение тока происходит по гармоническому закону, то изменение тока во вторичной катушке, а, следовательно, и э.д.с. так же происходит по гармоническому закону, поэтому решением уравнения (13) будет выражение вида:
,
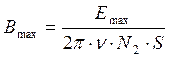(14)
где Вmax – амплитудное значение индукции магнитного поля;
Emax – амплитудное значение э.д.с. во вторичной катушке;
n - частота колебаний.
Эффективное значение э.д.с.
индукции во вторичной обмотке фиксируется вольтметром. Переходя к максимальному
значению можно написать, что 
.
Тогда индукцию Вmaxможно найти из
формулы
.
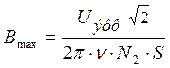(15)
Исходя из соотношения (7) можно получить значение магнитной проницаемости ферромагнитного образца
.
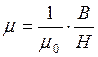(16)
Согласно теореме Лагранжа, если функция f(x) непрерывна на отрезке [a,b] и дифференцируемая на интервале (a,b), то на этом интервале найдутся, хоть одна точка с а< сb, такая, что
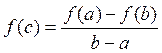. (17)
Сопоставив два выражения (16) и (17) для дифференциальной магнитной проницаемости получим:
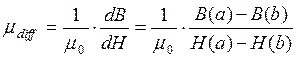. (19)
Таким образом из графика зависимости В =f(H) можно построить график функции m =f(H) воспользовавшись теоремой Лагранжа. Аналогично можно построить и зависимость mэфф =f(H).
Из соотношения (8) можно получить зависимость вектора намагниченности J от напряженности внешнего поля Н используя экспериментальные данные.
ВЫПОЛНЕНИЕ РАБОТЫ
1. Заготовить таблицу:
|
№ п/п |
I (Ma) |
U (B) |
B (Tл) |
H (A/м) |
J (А/м) |
m |
2. Снять зависимость выходного напряжения от тока первичной катушки (не менее 10 точек).
3. Рассчитать по данным эксперимента значения магнитной индукции, напряженности магнитного поля, вектора намагниченности по соотношениям (10), (8) и (15).
4. Построить график функций
B = f(H), mэфф = f(H), mдифф= f(H), J = f(H)
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какие вещества называются магнетиками? Виды магнетиков.
2. Дать определение магнитной индукции и напряженности магнитного поля.
3. Что такое магнитная проницаемость? Виды магнитной проницаемости.
4. Особенности ферромагнитных материалов.
5. Что означают магнитомягкие и жесткие ферромагнетики? Область применения.
mэфф = f(H), mдифф= f(H),.
ЛИТЕРАТУРА
1. Д.В. Сивухин. Общий курс физики. Т.3. Электричество. М.: Наука. 1977. С. 304-332
2. И.Е. Тамм. Основы теории электричества. М.: Наука. 1989. С. 227-283.
3. И.В. Савельев. Курс общей физики. Т.2. М.: Наука. 1988. С.153-180.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.