Расчет сложных цепей переменного тока. Линейные электрические цепи синусоидального тока/

Дальневосточный государственный

аграрный университет

Кафедра электротехники и электрических машин

Расчетно-графическое задание

Тема: «Расчет сложных цепей переменного тока»

Выполнил: студент I курса 7145 гр. ИЭАСХ

Дроздов А.В.

Проверил:

заведующий кафедрой, доцент

Мельников А.С.

Благовещенск

2006

Задача 1.2 Линейные электрические цепи синусоидального тока

Дана электрическая схема (рис. 1), выполнить следующее:

1) определить токи во всех ветвях цепи и напряжения на отдельных участках цепи. Найти комплексы действующих значений токов во всех ветвях и их мгновенные значения;

2) составить баланс мощностей (активной, реактивной, полной);

3) построить в масштабе на комплексной плоскости топографическую диаграмму напряжений для замкнутых контуров, совмещенную с векторной диаграммой токов;

4) определить показания вольтметра и ваттметра;

5) построить графики мгновенных значений тока и напряжения, подведенных к ваттметру.

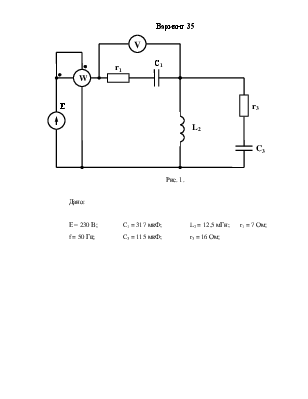
Вариант 35

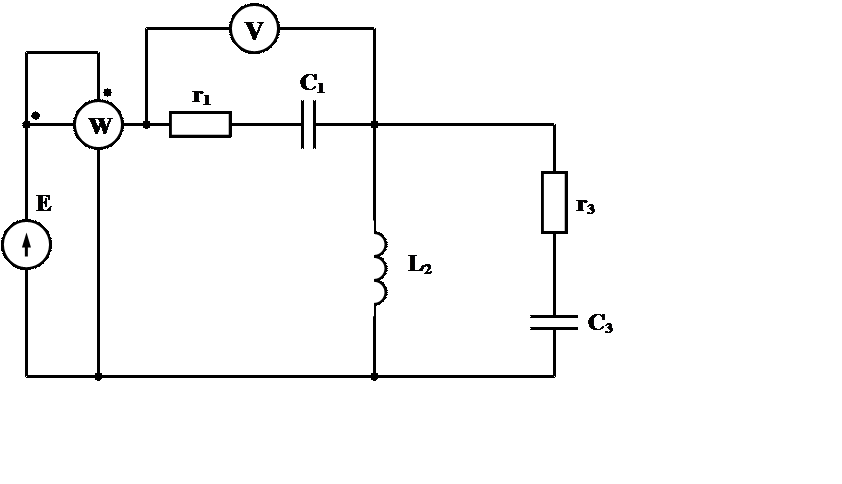
Рис. 1.

Дано:

Е = 230 В;               C₁ = 317 мкФ;                L₂ = 12,5 мГн;      r₁ = 7 Ом;

f = 50 Гц;                C₃ = 115 мкФ;                r₃ = 16 Ом;

Наиболее распространенным методом расчета таких цепей является метод эквивалентных преобразований. Этот метод заключается в последовательной, начиная с конца схемы, замене сопротивлений всех элементов электрической цепи одним эквивалентным с последующим использованием закона Ома.

Определим сопротивления реактивных элементов цепи:

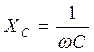; , где ω = 2πf = 2∙3,14∙50 = 314 с^-1 – угловая частота.

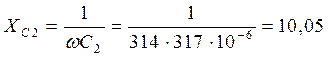 Ом;

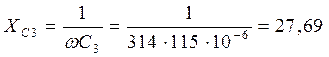 Ом;

 Ом.

Расчет выполняем в комплексной форме с последующим переходом к аналитическим выражениям токов в следующей последовательности:

1. Задаемся положительным направлением токов в ветвях цепи;

2. Записываем электрические сопротивления ветвей цепи в комплексной форме:

 Ом;

 Ом;

Ом.

Модуль и аргумент комплексного сопротивления ветвей цепи определяются по формулам

,  .

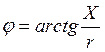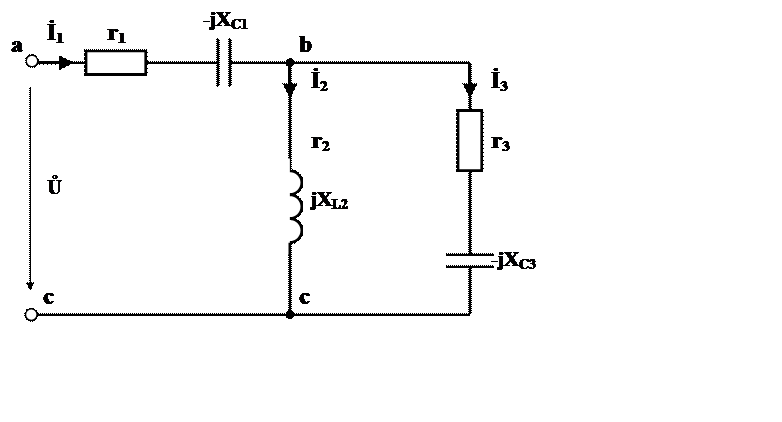
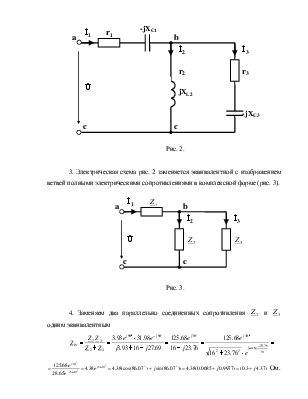
Рис. 2.

3. Электрическая схема рис. 2 заменяется эквивалентной с изображением ветвей полными электрическими сопротивлениями в комплексной форме (рис. 3).

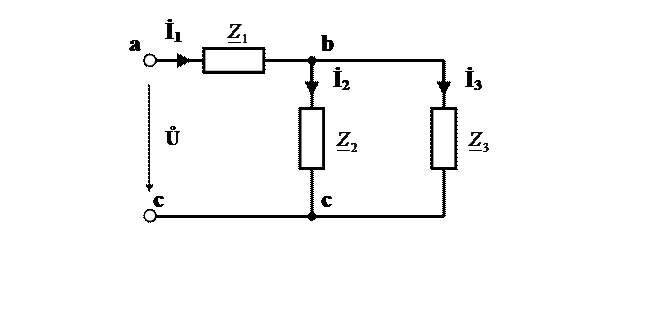
Рис. 3.

4. Заменяем два параллельно соединенных сопротивления  и  одним эквивалентным

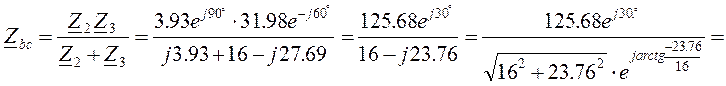
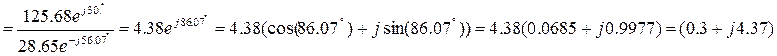 Ом.

5. Эквивалентное сопротивление всей цепи

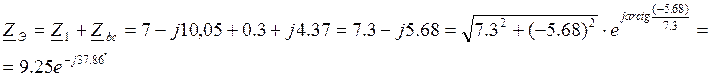 Ом.

6. Находим ток на входе цепи

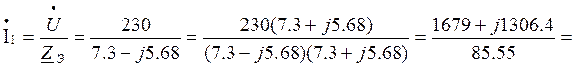
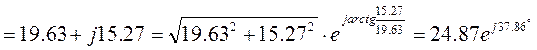 А.

7. Для определения токов  и  найдем напряжение . Это напряжение можно найти двумя способами:

а) по закону Ома

 В;

б) по второму закону Кирхгофа

 В;

8. Токи в параллельных ветвях

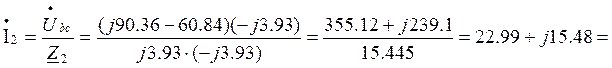
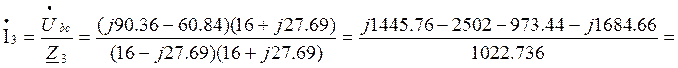
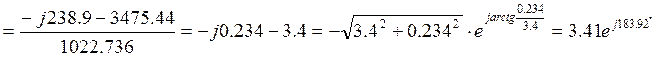 А;

 А.

9. Проверяем правильность расчета по первому и второму закону Кирхгофа:

по первому закону Кирхгофа имеем , то есть

 А – верно с учетом погрешности.

по второму закону Кирхгофа, для «abcda»

В.
2. Составление баланса мощностей

Баланс мощностей заключается в равенстве суммарных, отдаваемых источником электрической энергии и потребляемых электрофизическими элементами электрической цепи

, где  - сумма комплексных мощностей источников электрической энергии;

 - сумма комплексных мощностей электрофизических элементов электрической цепи.

Для нашей электрической цепи

 В;

ВА.

Активная мощность Р = 4515,72 Вт;

Реактивная мощность Q = 3507,47 вар.

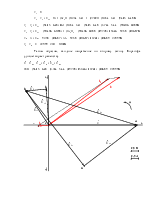
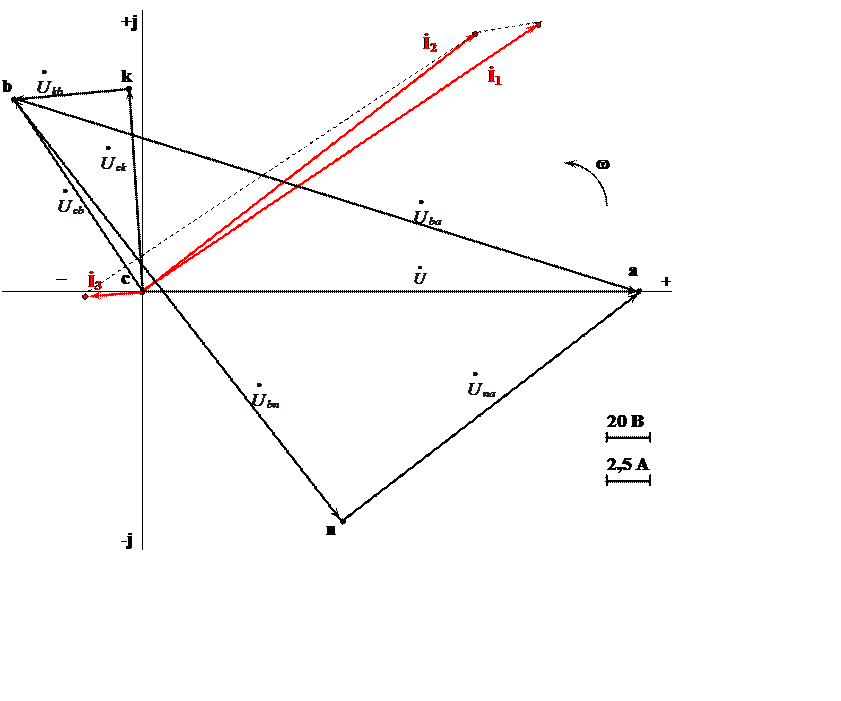
3. Построение в масштабе на комплексной плоскости топографической диаграммы напряжений для замкнутых контуров, совмещенной с векторной диаграммой токов

Откладываем в масштабе векторы токов I₁, I₂, I₃ на комплексной плоскости. Для суждения о напряжениях между различными точками электрической цепи строим топографическую диаграмму в масштабе напряжения. Топографическая диаграмма строится из замкнутого контура, идя против направления тока в элементах цепи. Все векторы падений напряжений на элементах цепи замкнутого контура имеют определенное направление (рис. 4):  - отстает от тока İ₃ на 90°;  - совпадает по фазе с током İ₃;  - отстает от тока İ₁ на 90°;  - совпадает по фазе с током İ₁.  - опережает ток İ₂ на 90°.

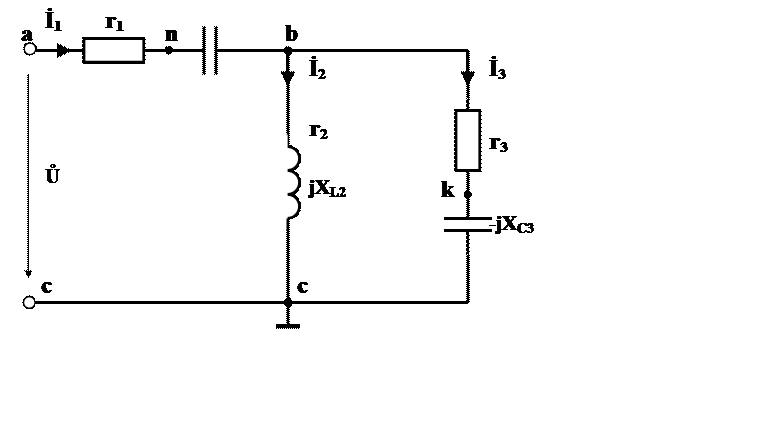
Рис. 4.

Совмещенная векторная диаграмма токов и топографическая диаграмма напряжений представлена на рисунке 5.

В

В

В

В

В

Таким образом, входное напряжение по второму закону Кирхгофа удовлетворяет равенству

В

4. Определение показания вольтметра и ваттметра

При аналитическом определении показаний приборов (вольтметров, амперметров, ваттметров) необходимо соответствующие расчеты выполнять в комплексах Действующих значений токов и напряжений. Показания приборов определяются модулем комплекса соответствующей электрической величины.

Показание вольтметра определяем из уравнения, составленного по второму закону Кирхгофа для контура «abca» (рис. 1).

, откуда

 В.

Показание вольтметра U_v = 304,55 В.

Ваттметр показывает активную мощность

, где U и I – действующие значения напряжения и тока;

φ – угол сдвига по фазе между напряжением и током.

При определении показания ваттметра необходимо учитывать ориентацию тока и напряжения относительно к генераторным зажимам (зажимам, обозначенным звездочками).

В нашем случае одинаково ориентированы относительно зажимов, обозначенных звездочками.

Ток  А.

Напряжение  В.

Сдвиг по фазе между векторами напряжения и тока

.

Показания ваттметра равно

 Вт.

Можно определить показание ваттметра через комплексную мощность

, где  – комплекс напряжения, приложенного к ваттметру, В;

 – сопряженный комплекс тока, протекающего через токовую обмотку ваттметра, А.

Используем алгебраическую форму записи комплекса напряжения и тока

 В,

 А,

 ВА

Показание ваттметра равно действительной части комплексной мощности

 Вт.

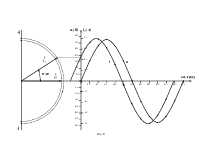
5. Построение графиков мгновенных значений тока и напряжения, подведенных к ваттметру

Для построения временных характеристик тока и напряжения, подведенных к ваттметру, запишем их мгновенные значения

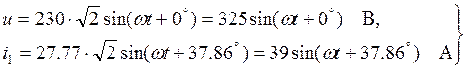
Для расчета координат точек кривых i₁ = f₁(ωt) и u = f₂(ωt) составляем таблицу 1.

Таблица 1.

Временные характеристики тока i₁ = f₁(ωt) и напряжения u = f₂(ωt) приведены на рисунке 6.