Вычисление среднего арифметического отклонения заболеваемости (летальности, иммунизации)

Лабораторное занятие №7

Тема: Вычисление среднего арифметического отклонения заболеваемости (летальности, иммунизации)

Цель – научиться изучать величину средней арифметической и ее ошибки.

Задачи:

1.  Изучить основные обозначения.

2.  Построить основную и вспомогательную таблицы.

3.  Вычислить величину средней арифметической.

4.  Вычислить величину ошибки средней арифметической.

Вариационная статистика – наука, разрабатывающая изучение метода варьирующего признака на массовых материалах в различных областях знания. Варьирующими признаками принято называть такие, которые проявляют определенную закономерность в изменчивости значений.

В качестве варьирующих могут быть такие показатели развития эпизоотического процесса, как количество неблагополучных пунктов, коэффициент очаговости, заболеваемость, летальность, уровень вакцинации животных и так далее. Взятые за ряд лет по годам и связанные в определенные таблицы.

При переработки показателей эпизоотического процесса, для вычисления средней арифметической, среднего квадратического отклонения, ошибки средней арифметической, критерия средней арифметической, критерия достоверности и вероятности, варьирующие величины обозначаются специальными терминами, символами, принятыми в вариационной статистике.

Основные обозначения:

V(X) – величина варьирующего признака (показатель);

n – число варьирующих признаков (показателей, участвующих в обработке);

Σ (большая греческая сигма) – общепринятое обозначение арифметического           действия (суммы);

() – среднее арифметическое варьирующих признаков (показателей участвующих в обработке);

 (S) – сигма малая, показатель среднего квадратического отклонения;

m (Sx) – искомая ошибка средней арифметической;

n-1=V – число степеней свободы; (ню)

t – критерий достоверности (существенности);

P –уровень вероятности (существенности);

r – коэффициент парной корреляции;

R – коэффициент множественной корреляции;

Таблица 28.

Заболеваемость лептоспирозом крупного рогатого скота в России

в 2001-2010 гг. (количество заболевших животных на 10 тысяч поголовья)

Край	Годы										Средний показатель за  10 лет M±m	p
	2001	2002	2003	2004	2005	2006	2007	2008	2009	2010
	1	2	3	4	5	6	7	8	9	10
Хабаровский	3,41	4,89	4,49	5,54	3,61	1,80	1,83	1,08	1,24	0,80	2,87±0,58	<0,001
Красноярский	3,44	2,0	2,63	3,33	1,83	1,19	0,91	0,43	0,36	0,28	1,69±0,41	<0,001
Краснодарский	4,33	3,58	5,95	1,91	1,03	0,32	0,28	0,51	0,12	0,64	1,86±0,68	<0,001

Таблица 29.

Разброс вариационного ряда по заболеваемости крупного рогатого скота лептоспирозом по Хабаровскому краю

n	V	V-M	(V-M)²
1	3.41	0.54	0.29
2	4.89	2.02	4.08
3	4.49	1.62	2.62
4	5.54	2.67	7.13
5	3.61	0.74	0.55
6	1.80	-1.07	1.14
7	1.83	-1.04	1.08
8	1.08	-1.79	3.20
9	1.24	-1.63	2.66
10	0.8	-2.07	4.28
n=10	Σv=28.69 M=2.87		Σ(V-M)²=27.05

Из приведенного примера видно, что число показателей (n) равно 10. Следовательно, число вариантов (показателей заболеваемости, анализ за 2001-2010 гг.) также равно 10.

Вычисление средней арифметической (М)

Средняя арифметическая определяется путем деления суммы (ΣV) вариантов на число вариантов, участвующих в обработке (п) по формуле:

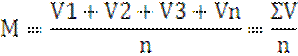
На нашем примере общая сумма вариантов (показателей) ΣV равна 28,69 откуда средняя арифметическая составит:

М=

Вычисление среднего квадратического отклонения:

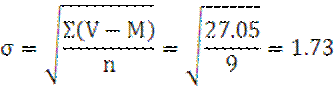
m=±

М±m=2.87±0.58

Таблица 30.

Разброс вариационного ряда по заболеваемости крупного рогатого скота лептоспирозом в Красноярском крае

№	V	V-M	(V-M)²
1	3,44	1,80	3,24
2	2,00	0,36	0,13
3	2,63	0,99	0,98
4	3,33	1,69	2,86
5	1,87	0,19	0,04
6	1,19	-0,45	0,20
7	0,91	-0,73	0,53
8	0,43	-1,21	1,46
9	0,36	-1,28	1,64
10	0,28	-1,36	1,85
n=10	Σv M=1,64		Σ(V-M)²=12,93

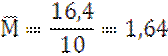
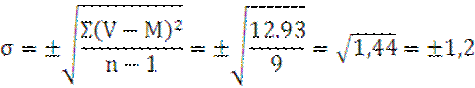
m=±

M±m=1.64 ± 0.4

Таблица 31.

Разброс вариационного ряда по заболеваемости крупного рогатого скота лептоспирозом в Краснодарском крае

№	V	V-M	(V-M)²
1	4,33	2,46	6,05
2	3,58	1,71	2,92
3	5,95	4,08	16,65
4	1,91	0,04	0,01
5	1,03	-0,84	0,70
6	0,32	-1,55	2,40
7	0,28	-1,59	2,53
8	0,51	1,36	1,85
9	0,12	1,75	3,06
10	0,64	1,23	1,51
n=10	Σv=18,67 M=1,87		Σ(V-M)²=37,68

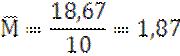
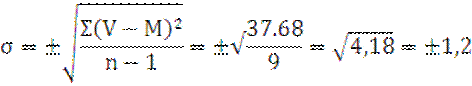
m=±

M±m=1,87 ± 0.68

Вычисление ошибки средней арифметической (М)

При малом числе показателей, участвующих в обработке (п<30) ошибку средней арифметической определяют по формуле:

M=±  а при 30 m = ±

В нашем примере: m= ±

Среднюю арифметическую принято записывать с ее ошибкой:M±m

Ошибка средней арифметической дает возможность:

1.  Определить в каких пределах находится средняя величина. Выборочные статистические величины правильно отражают свойства генеральной совокупности, если ошибка (m) укладывается в своей средней (М) не менее двух раз.

2.  Выяснить степень достоверности между двумя сравниваемыми выборочными средними.

Таким образом, в нашем примере средняя арифметическая М=2,87, ошибка средней арифметической m=±0,58. Средний показатель за 10 лет при этих данных будет М±m = 2.87±0.58 (по Хабаровскому краю). Средний показатель заболеваемости крупного рогатого скота лептоспирозом в Красноярском крае M±m = 1.64±0.40, Красноярском крае M±m = 1.64±0.68.

Контрольные вопросы:

1.  Основные обозначения величин.

2.  Что означает средняя арифметическая величина и ее формула.

3.  Вычислить среднюю арифметическую величину.

4.  Что означает ошибка средней арифметической, ее формула.

5.  Вычислить ошибку средней арифметической на конкретном примере.