Вычисление среднего квадратического отклонения заболеваемости (летальности, иммунизации) (Лабораторное занятие № 8)

Лабораторное занятие №8

Тема: Вычисление среднего квадратического отклонения ( заболеваемости (летальности, иммунизации)

Цель – научиться вычислять среднее квадратическое отклонение.

Задачи:

1.  Определить величину дисперсии.

2.  Изучить формулу  – среднего квадратического отклонения.

3.  Определить среднее квадратическое отклонение на табличном материале.

Среднее квадратическое отклонение является основным критерием изменчивости. Оно показывает насколько в среднем каждый вариант (V) отклоняется больше (+) или меньше (-) от средней арифметической (М). В таблице вариационного ряда показаны величины разницы между средней арифметической и каждым вариантом (V-М). Для вычисления среднего квадратического отклонения, каждое значение (V-M)². Затем показатели     (V-М)² - графы 4 (таблица) суммируют. Сумма квадратов отклонений       Σ(V-M)² то есть сумма квадратов разностей между каждым вариантом и средней арифметической в нашем примере составила 27,05(см. табл.).

Если число вариантов (показателей), участвующих в обработке, меньше 30 (n<30), как в нашем примере, то величину дисперсии отыскивают путем деления суммы квадратов отклонений (Σ(V-M)²) на число вариантов минус один:

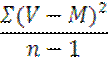
Если число вариантов больше 30 (n>30), то единицу не вычитают:

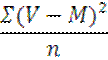
В нашем примере показатель дисперсии будет равен:

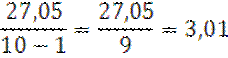
Среднее квадратическое отклонение ( определяют путем извлечения квадратного корня из показателя дисперсии (изменчивости) с точностью на один знак больше, чем средняя арифметическая и выражают в тех же единицах, как и среднюю арифметическую.

Среднее квадратическое отклонение при малом числе показателей (n<30) рассчитывают по формуле:

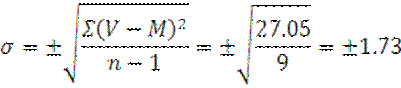
Чем больше значение а, тем больше изменчивость изучаемого признака в совокупности, чем меньше а, тем меньше изменчивость  признаков, тем теснее и типичнее вычислена в этом ряду средняя. В так называемых нормальных вариационных рядах, отклонение (крайние показатели в выборке, то есть это максимальное и минимальное значение признака, показывающее размах разнообразия) от средней арифметической должно быть на более ± 3.

Отклонения отдельных вариантов ряда от средней арифметической (может быть определено по формуле:

±

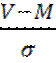
В нашем примере максимальная варианта (5,54-показатель заболеваемости за 2003) больше средней арифметической на 1,5

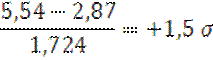
Минимальная варианта (0,80 – в 2008г.) меньше средней арифметической на 1,2.

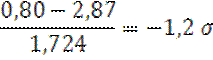
Если какой–либо показатель в выборке отклоняется от средней арифметической более чем на 3  то значит, он попал в выборку случайно или возник под влиянием каких-то специфических факторов, особых условий.

Контрольные вопросы

1.  Дать характеристику понятия «средне квадратическое отклонение».

2.  Расчет среднего квадратического отклонения.

3.  Расчет величины дисперсии.