Определение ЭДС неизвестного источника методом компенсации: Методические указания к лабораторной работе № 217 по дисциплине «Физика», страница 2

E_X = IR_X.                                                (6)

Затем необходимо произвести ещё одно измерение, подключив в установке вместо E_X «стандартный элемент» – источник E_N ЭДС которого известна с высокой точностью. Контакт D переводят в новое положение D`, в котором гальванометр вновь не регистрирует тока. В этом положении справедливо равенство:

E_N = IR_N,                                                 (7)

где R_N – сопротивление между точками А и D`. Так как через резистор R протекает ток той же величины I, то:

 = ,

или

 = ,

откуда:

E_X = E_N.                                             (8)

Так как резистор R представляет собой однородную проволоку, то сопротивления R_X и R_N пропорциональны соответствующим длинам плеч реохорда l_X и l_N, поэтому окончательно получаем:

E_X = E_N.                                             (9)

Следовательно, экспериментально определив длины плеч реохорда в двух случаях – в случае включения в компенсационную схему источника с неизвестной ЭДС E_X и в случае включения источника с известной ЭДС E_N можно по формуле (9) рассчитать ЭДС неизвестного источника E_X. В компенсационном методе роль измерительного прибора, гальванометра сводится не к измерению тока, а к установлению его отсутствия на участке цени с источником неизвестной ЭДС. Поэтому в компенсационных схемах применяются не точные, но очень чувствительные гальванометры (так называемые ноль-гальванометры).

Общий вид лабораторной установки представлен на рис. 3.

Рис. 3.

Порядок выполнения работы

1. Ознакомиться с принципом работы компенсационной схемы и её применением в данной лабораторной работе, т. е. с монтажной компенсационной схемой, представленной на рис. 4. Здесь К1 – ключ включения источника вспомогательного питанияE, К2 – переключатель для ввода в цепь попеременно исследуемого и эталонного источников ЭДС. В лабораторной установке реохорд АВ заменен потенциометром АВ с движком D. При этом выводы расчётной формулы (9) остаются справедливыми. Остальные обозначения соответствуют обозначениям схемы, представленной на рис. 2.

2. Ознакомиться с эксплуатационными особенностями схемы (см. последующие пункты).

3. Замкнуть переключатель К2 (двойной ключ со средним положением) на исследуемый элемент E_X.

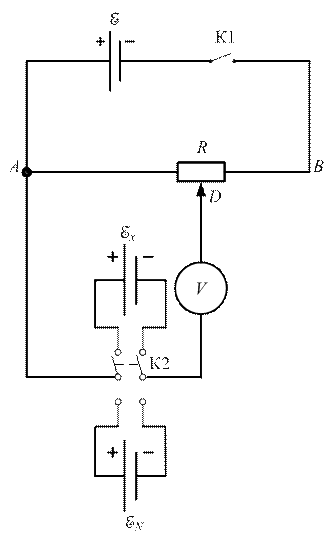
Рис. 4.

4. Замкнуть ключ К1 и удерживать его в течение измерения.

Замыкание ключей необходимо производить только в указанном порядке.

Цепь должна замыкаться только на короткое время во избежание неэкономного расходования источника напряжения.

5. Добившись полного отсутствия тока в цепи вольтметра V передвижением подвижного контакта потенциометра, произвести измерение l_X с помощью линейки, установленной на потенциометре. Аналогичным образом измерить l_N, замкнув элемент E_N ключом К2. Измерения проделать 4 (четыре) раза. Найти средние значения l_X и l_N. Полученные данные занести в таблицу1.

6. По окончании работы переключатель К2 обязательно поставить в среднее (нейтральное) положение!

7. Рассчитать значение E_Xпо формуле (9), используя средние значения l_{X СР} и l_{N СР}, и занести результат в таблицу 1.

Таблица 1

8. Определить предельную относительную погрешность измерений по формуле:

δE =  = 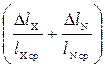,                               (10)

считая, что в данной работе преобладают приборные ошибки, определяющиеся ценой деления линейки, установленной на потенциометре. Запишите окончательный результат в виде:

E_X= E_Xср ± ΔE_X.

Контрольные вопросы

1.  В чем заключается суть метода компенсации? Зарисовать схему цепи.

2.  Какие преимущества имеет метод компенсации по сравнению с другими методами измерения ЭДС?

3.  Сформулировать закон Ома для замкнутой цепи, участка цепи, содержащего ЭДС и участка цепи, не содержащего ЭДС.

4.  Что называется ЭДС?

5.  Что называется напряжением?

6.  В каких единицах измеряются ЭДС и напряжение в международной системе единиц?

7.  Может ли резистор обладать ЭДС?

8.  Может ли напряжение на клеммах батареи превышать её ЭДС?

Список литературы

1.  Савельев И.В. Курс общей физики. Книга 2. Электричество и магнетизм. − М.: ООО «Издательство Астрель»: ООО «Издательство АСТ», 2002.

2.  Яворский Б.М., Детлаф А.А. Курс физики. – М.: Изд-во «Академия», 2003. – 720 с.

3.  Трофимова Т.И. Курс физики. – М.: Высшая школа, 2004. – 544 с.

4.  Селезнёв В.А., Тимофеев Ю.П. Методические указания к вводному занятию в лабораториях кафедры физики. – М.: МИИТ, 2006. – 30 с.

5.  Андреев А.И., Государева Н.А., Кушко А.Н. Физика. Методические указания к лабораторным работам 13, 14, 16, 17, 18 // – М.: МИИТ, 2008. – 48 с.

Учебно-методическое издание

Кули-Заде Тофик Салман-Оглы

Васильев Евгений Васильевич

ОПРЕДЕЛЕНИЕ ЭДС НЕИЗВЕСТНОГО

ИСТОЧНИКА МЕТОДОМ КОМПЕНСАЦИИ

Методические указания к лабораторной работе №217

под редакцией доцента Харитонова Ю.Н.

127994, Москва, ул. Образцова д. 9, стр. 9.

Типография МИИТа