Соотношение неопределенностей для фотонов (Теоретическое введение к лабораторной работе. Порядок выполнения работы)

Лабораторная работа

Соотношение неопределенностей для фотонов

Цель работы: экспериментальная проверка выполнения соотношения неопределенностей для фотонов.

Приборы и принадлежности: источники излучения (лазеры ЛГН-113 и       ZY 852), щель с микрометрической регулировкой ширины, оптическая скамья, экран, линейка рулетка.

Теоретическое введение

Принцип неопределенностей, сформулированный на основе корпускулярно-волнового дуализма, является одним из фундаментальных принципов современной физики. Для квантовых частиц его можно сформулировать следующим образом. Неопределенность координатной составляющей частицы  и неопределенность проекции импульса на то же направление  удовлетворяют соотношению

 ,                                                 (1)

где  – постоянная Планка.

В данной работе соотношение неопределенности (1) проверяется экспериментально для фотонов. Как проявление принципа неопределенности в оптике можно трактовать явление дифракции. Действительно, состояние движения фотона вдоль оси  в области  (рисунок 1) ничем не ограничено в пространстве. В этой области координат импульс фотона  характеризуется вполне конкретными значениями координатных составляющих . В точке , в которой расположена входная щель, состояние движения фотона характеризуется пространственным ограничением по координате . Неопределенность координаты фотона , задаваемая шириной входной щели, обусловливает в соответствии с формулой (1) неопределенность соответствующей координатной составляющей импульса  в окрестности значения . Следовательно, в области пространства  будут присутствовать фотоны, которые движутся не только в направлении оси , но и под некоторым углом a к ней, чем и объясняется явление дифракции пучка излучения с точки зрения квантовой теории.

Поскольку неопределенность проекции импульса  определяет отличие    - ой компоненты импульса от нулевого значения, то можно записать

.                                                         (2)

Учтем, что модуль импульса фотона излучения с длиной волны  определяется

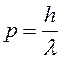.                                                                (3)

Тогда величину неопределенности импульса (2) можно записать

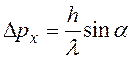 .                                                           (4)

Так как при дифракции основная доля излучения будет сосредоточена в максимуме нулевого порядка, то есть в диапазоне угловых расстояний от () до  (рисунок 1), то неопределенность выделенной проекции импульса можно принять равной . При этом произведение неопределенностей координаты и импульса будет удовлетворять соотношению

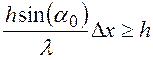,   или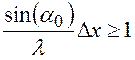   

Из этого неравенства следует, что угловая расходимость светового пучка после дифракции на щели шириной Dх может быть оценена на основе равенства

.                                                      (5)

Этот результат полностью соответствует результату классической теории дифракции, в которой расходимость излучения определяется на основе формулы .

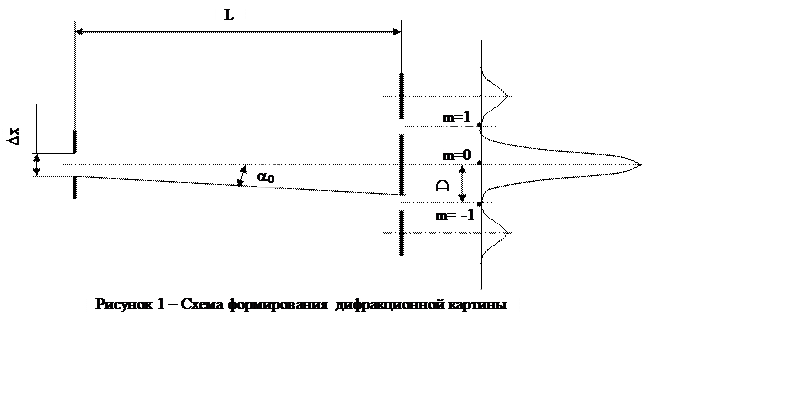
В формуле (5) угол  определяет направления на первые минимумы в дифракционной картине, расстояние на экране между которыми составляет (см. рисунок 1). Ввиду малости угла  можно записать

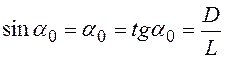.                                             (6)

Сравнив формулы (5) и (6), получим выражение

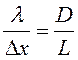, которое для удобства анализа представим в виде

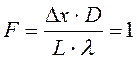.                                                             (7)

Таким образом, для проверки выполнения соотношения неопределенностей необходимо измерить ширину щели, принимаемую за неопределенность координаты фотона , ширину центрального максимума (расстояние между минимумами +1 и -1 порядков) в дифракционной картине  и расстояние от щели до экрана .

Порядок выполнения работы

Установка для проверки принципа неопределенностей (рисунок 2) состоит из источника монохроматического излучения 1, щели 2, ширина которой устанавливается и измеряется с помощью микрометрического винта, и экрана со шкалой 3, расположенных на оптической скамье 4.

Испускаемый лазерным источником пучок излучения проходит через щель и попадает на экран, где наблюдается исследуемая дифракционная картина (см. рисунок 1). Изменяя ширину щели посредством вращения микрометрического винта барабана, а также расстояние между щелью и экраном , можно наблюдать изменение вида дифракционной картины.