Задания к лабораторному (компьютерному) практикуму по дисциплине "Информатика и программирование" (Найти минимальный элемент двумерной таблицы и указать его номер. Составить программу, определяющую заданный период времени)

вычислить и напечатать удвоенный куб первого числа, в противном случае напечатать оба числа.

Задание 35

Дано одно число. Если и синус, и косинус этого числа больше 0.3, то вычислить и напечатать квадрат этого числа, в противном случае его куб.

Задание 36

Даны 4 числа. Если сумма первых 2-х чисел больше 2-х последних, то вычислить и напечатать тангенс 3-его числа. В противном случае напечатать синус первого числа.

Задание 37

Даны 3 числа. Если среди них нет нулей, то вычислить и напечатать произведение этих чисел. В противном случае – их утроенную сумму.

Задание 38

Дано 2 числа. Вычислить их сумму. Если она превышает  1000, то вычислить и напечатать квадрат первого числа. В противном случае – квадрат второго.

Задание 39

Дано 4 числа. Если среди них найдется число 999, то напечатать все четыре числа, в противном случае – сумму 2-х последних.

Задание 40

Дано одно число. Вычислить его квадрат и синус. Если синус числа положительный, то вычислить и напечатать его удвоенный тангенс. В противном случае – утроенный косинус.

Задание 41

Дано 3 числа. Если все они отрицательные, то вычислить и напечатать куб второго числа, в противном случае – произведение 2-х первых чисел .

Задание 42

Дано 2 числа. Вычислить квадрат 2-го числа. Если он превышает 300, вычислить и напечатать квадрат первого числа, в противном случае – напечатать второе число.

Задание 43

Даны две заштрихованные области и точка М(х₁,у₁). Куда попадает точка: в верхнюю заштрихованную область; в нижнюю заштрихованную область и попадает мимо областей.

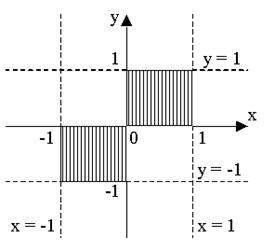
Задание 44

Даны две заштрихованные области и точка М(х₁,у₁). Куда попадает точка: в верхнюю заштрихованную область; в нижнюю заштрихованную область и попадает мимо областей.

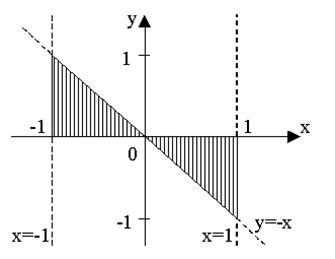
Задание 45

Даны две заштрихованные области и точка М(х₁,у₁). Куда попадает точка: в верхнюю заштрихованную область; в нижнюю заштрихованную область и попадает мимо областей.

Задание 46

Даны две заштрихованные области и точка М(х₁,у₁). Куда попадает точка: в верхнюю заштрихованную область; в нижнюю заштрихованную область и попадает мимо областей.

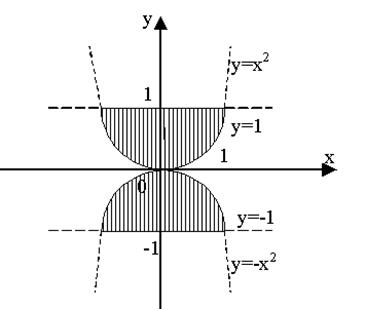
Задание 47

Даны две заштрихованные области и точка М(х₁,у₁). Куда попадает точка: в верхнюю заштрихованную область; в нижнюю заштрихованную область и попадает мимо областей.

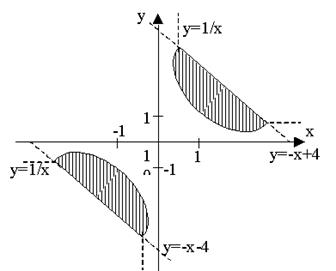
Задание 48

Даны две заштрихованные области и точка М(х₁,у₁). Куда попадает точка: в верхнюю заштрихованную область; в нижнюю заштрихованную область и попадает мимо областей.

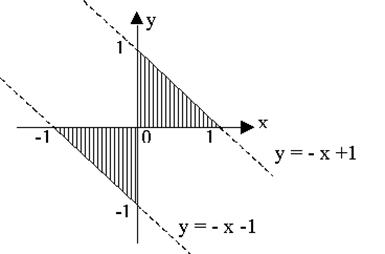
Задание 49

Даны две заштрихованные области и точка М(х₁,у₁). Куда попадает точка: в верхнюю заштрихованную область; в нижнюю заштрихованную область и попадает мимо областей.

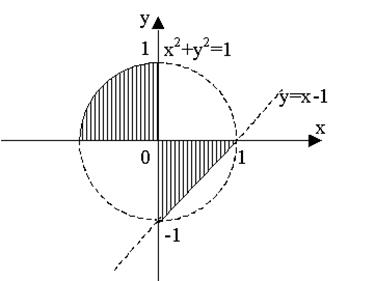
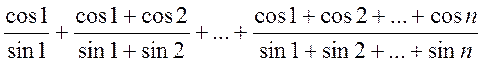Задание 50

где n – любое натуральное число.

Задание 51

Вычислить: 

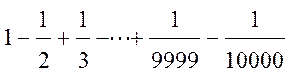
Задание 52

Вычислить: x+(x^2)/2!+(x^3)/3!+(x^4)/4!+(x^5)/5!

Задание 53

Вычислить: x-(x^2)/2!+(x^3)/3!-(x^4)/4!+(x^5)/5!

Задание 54

Вычислить:   x-(x^3)/3!+(x^5)/5!-(x^7)/7!+(x^9)/9!,

где x – любое вещественное число.

Задание 55

Дано натуральное число  n. Вычислить произведение первых n сомножителей:        

Задание 56

Дано натуральное число x. Вычислить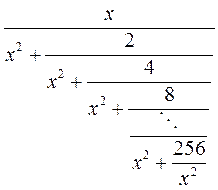

Задание 57

Дано натуральное число n. Как наименьшим количеством денежных купюр можно выплатить n рублей? Предполагается, что в достаточном количестве имеются купюры достоинством 1, 2, 5, 10, 50, 100 и 500 рублей.

Задание 58

Дано натуральное число n из пяти цифр. Определить, входит ли цифра 3 в запись числа n.

Задание 59

Определить, сколько счастливых билетов в трамвайном рулоне (полагаем, что рулон содержит билеты с номерами в интервале от 000000 до 999999), а счастливым считается билет, сумма первых трех цифр которого равна сумме трех последних цифр. Например: 321231, 126009 и т.д.

Задание 60

Определить суммарный объем в метрах двенадцати вложенных друг в друга шаров со стенками 5 мм. Внутренний диаметр внутреннего шара равен 10 мм. Считать, что шары вкладываются друг в друга без зазоров.

Задание 61

Изобретатель шахмат попросил в качестве вознаграждения заполнить клетки шахматной доски зернами риса, причем класть на первую клетку одно зернышко, на вторую – два, на третью – четыре, на следующую – 8 и т.д. Если весь этот рис ссыпать в мешки по 50 кг и уложить их рядом, то сколько раз получившаяся вереница мешков опояшет Землю? (Для справки: 1 г риса содержит 100 зерен, толщина заполненного мешка – 0,52 м, а окружность Земли – 40000 км).

Задание 62

Рассчитать траекторию движения снаряда по формулам X=Vx·t Y=Vy·t-g·t2/2 при постоянных скоростях Vx,Vy. Время t изменяется с постоянным шагом Dt. Закончить вычисления, когда снаряд упадет. В формулах приняты обозначения: X, Y — координаты траектории полета снаряда относительно поверхности земли, g — ускорение свободного падения.

Задание 63

Население двух стран равно H1 и H2, а прирост населения в процентах составляет  P1 и P2 соответственно. Если дано, что H1>H2 и P1< P2, то через сколько лет население второй страны превзойдет население первой страны.

Задание 64

Клиент банка "Нотериал" положил на свой счет 1000 долларов под 4% ежемесячных начислений. Через сколько полных лет сумма вклада клиенты превысит 3000 долларов?

Задание 65

Составить программу, определяющую период времени, необходимый для того, чтобы вложенный капитал возрос в три раза, при условии