Вывод уравнений составляющих электрического и магнитного поля высшей волны типа TE01

Вывод уравнений составляющих электрического и магнитного поля высшей волны типа TE₀₁.

Для расчёта полей в волноводе необходимо найти частные решения скалярного уравнения Гельмгольца, этот процесс очень трудоёмкий, мы воспользуемся готовыми формулами вывод который приведён в [1,с.72-79] :

Комплексная амплитуда продольной составляющей электрического поля :

Комплексная амплитуда поперечной составляющейэлектрического поля:

Комплексная амплитуда поперечной составляющеймагнитного поля:

x, y, z-орты; a,b –длинна широкой и узкой стенок волновода соответственно;B- коэффициент характеризующий интенсивность поля, определяется условиями возбуждения колебаний в волноводе или величиной мощности генераторного прибора, питающего волновод;mи n-индексы высшей волны; ρ_E-волновое сопротивление волновода на волне E-типа; k-собственное волновое число; γ-постоянная распространения волны; β-волновое число.

Собственное волновое число kдля высшей волны TE₀₁ будет равно:

Тогда критическая длинна волны:

Рассматривая передачу высокочастотной энергии по орту +z₀ (т.е. в положительном направлении оси z):

Преобразуем комплексную амплитудупоперечной составляющей электрического поля :

.

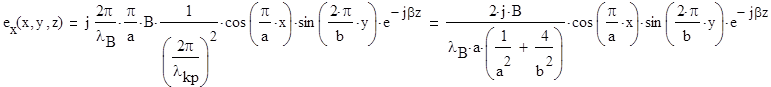Вводим комплексный коэффициент :

.

           .

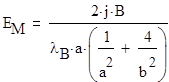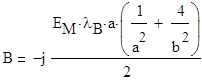Проделав аналогичные преобразования с уравнениями остальных составляющих получим:

.   

.

.

.                           

.                

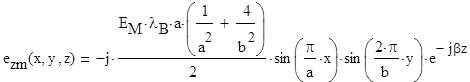
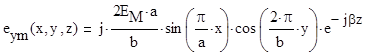
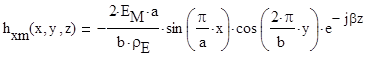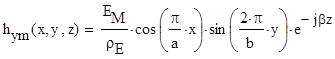Далее представим комплексный коэффициент Ė_M как Ė_M= E_Me^jφm, где E_M – модуль, φ_m – аргумент и положим, что φ_m=0.

Формируем соответствующие комплексные представления, используя полученные комплексные амплитуды, вводя множитель e^jωt, а затем, извлекая реальную часть, записываем уравнения для мгновенных значений проекций векторов Е и Н в прямоугольном волноводе для волны E₁₂:

Получим уравнения составляющих тока смещения:

J_см.m(x,y,z)=jωε₀ε_rĖ_M(x,y,z)=jωε₀ε_r[x₀ė_xm(x,y,z)+ y₀ė_ym(x,y,z)+ z₀ė_zm(x,y,z)]

При построении полей, зафиксируем момент времени t=0. Получим следующие распределения полей в волноводе:

 

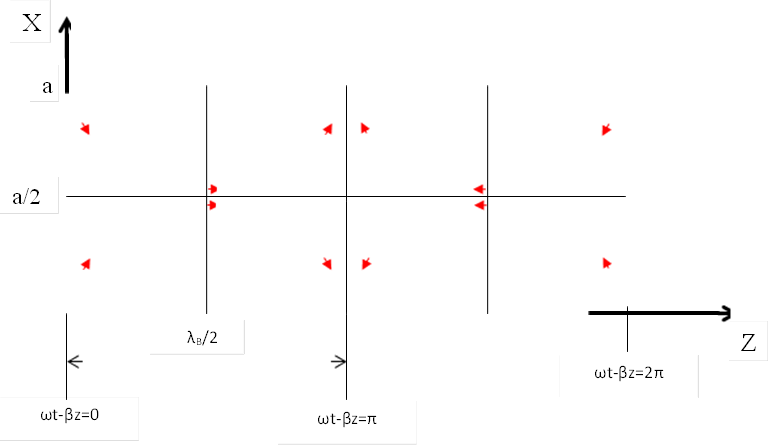
Рис.6. Cоставляющие по осям x и z электрического поля в сечении волновода y=b/4. При y=3b/4 направления векторов меняются на противоположные.

 

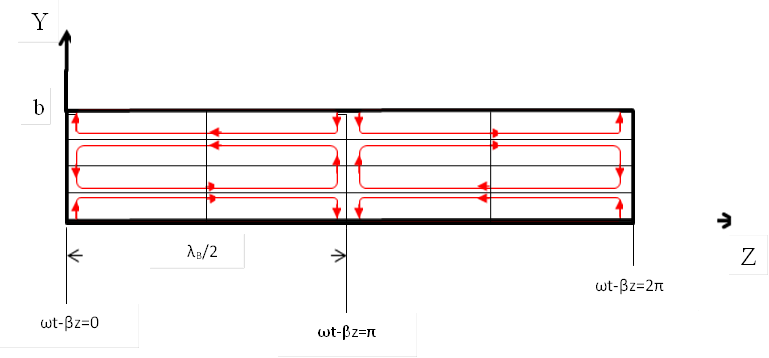
Рис.7. Cоставляющие по осям y и z электрического поля в сечении волновода x=a/2. При x=3a/2 направления векторов меняются на противоположные.

 

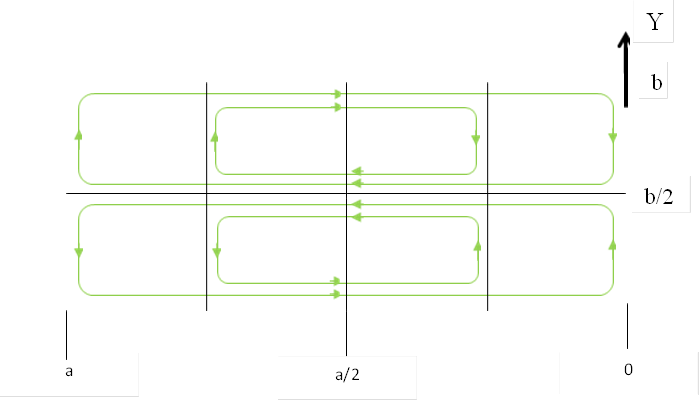
Рис.8. Cоставляющие по осям x и y магнитного поля в сечении волновода   ωt-βz=0. Направления векторов меняются на противоположные через каждую полуволну.