Анализ математической основы карт

                 МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ

Учреждение образования

«Гомельский государственный университет

имени Франциска Скорины»

Геолого-географический факультет

Кафедра экологии

СУРС по Картографии

Выполнила:

Студентка группы ГЭ-21                                                                                                   Володина О.Л.

Гомель 2011

Лабораторная работа №1

«Анализ математической основы карт»

Цель работы: Научиться определять соответствуют ли элементы математической основы назначению карты, возможно ли вести измерения по ней с заданной точностью, так же решать обратную задачу, т.е. определить масштаб и проекцию в которой должна создаться карта с определённым назначением или с заданной точностью измерений.

Теоретические вопросы: Анализ математической основы карт включает рассмотрение целесообразности следующих элементов:

1)  масштаба;

2)  проекции;

3)  координатной сетки;

4)  компоновки и системы разградки;

5)  системы координат и геодезической опорной сети (для топокарт).

Масштаб должен обеспечивать необходимую точность определения по карте координат и расстояний. Согласно принятой точности топокарт и планов, средние ошибки в положениях на картах и планах предметов, и твёрдых контуров относительно ближайших опорных  пунктов не должны превышать 0,5 мм. А в горных и пустынных районах 0,75 мм. В качестве предметных ошибок принимают удвоенные значения средних.

Если обозначим через mk средние ошибки в координатах точек, а через md средние ошибки в определении расстояний между ними, то для равнинных территорий будет иметь:

mk = ± 0,5 * N мм = ± 0,005 * N м (1).

md = ± 0,5 * N * 2 = ± 0,7 * N мм (2).

N- знаменатель численного масштаба заданной карты (масштаб карты).

Величину N  можно определить по выражениям:

N = 2000 * mk м (3);

N = 1415 * md м (4).

Таким образом установлен наименьший масштаб, который будет обеспечивать необходимую точность.

Карты крупнее данного масштаба будут удовлетворять поставленной нами точности.

Для требуемой точности измерения площадей, формула для знаменателя масштаба будет иметь следующий вид:

N =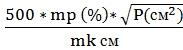 (5).

mp – средние ошибки в определении площадей.

mp = 100 *  (6).

p – величина анализируемой площади.

Кроме того масштаб должен обеспечивать нужную нагрузку (n) приходящуюся на 1дм²

n = M² * q  (7).

q – показатель густоты; М – именованный масштаб выражен числом км в 1см.

Оценить правильность выбора масштаба можно лишь зная требования вытекающие  из назначения карты. Проекция выбирается тоже в зависимости от назначения карты, с учётом искажений, которые она даёт. Так же конфигурации изображаемой территории.

На систему координат и особенности координатных сеток надо обращать особое внимание, если в дальнейшем топокарты будут использоваться в качестве картосоставительских источников.

Задание по работе:

1)  Определить с какой точностью можно вынести измерения по карте с заданной математической основой. И какому назначению она может соответствовать. Задание выполняется по вариантам, в каждом из которых должно быть 2 карты.

Название Карта Исходные данные	Математическая основа			Точность определения по      карте
	проекция	вид координатной сетки	масштаб	mk	md	mp(%)

2)  Установить математическую основу позволяющую вести измерения с заданной точностью, если:

mk = ± 25 м; ± 50 м; ± 100 м; ± 150 м.

mp = 1; 2; 3; 3,5.

р =  1 дм² = 100 см

Результаты оформить виде таблицы.

mk

N

md

mp(%)

N

3)  Определить масштаб карты для заданной густоты (q) и нагрузки (n) , для объектов локализированных по пунктам.

Результат оформить виде таблицы, если:

(q) = 26; 10; 5; 2.

(n) = 50; 100; 150; 200.

на 1 дм² карты.

n

q

М =

Лабораторная работа № 2

« Вычисление размеров искажений»

Цель работы: Научиться определять искажения на карте, используя математические формулы, понимать характер распределения искажений картографических проекций.

Теоретические вопросы:  Поверхность элипсойда нельзя развернуть в плоскость сравнением всех ограничений. В результате этой процедуры обязательно произойдут разрывы или перекрытие возникает необходимость проводить или сжатие определённых участков и следовательно появляются искажения в длинах, площадях, формах, углах, которые отсутствуют только в точках и линиях нулевых искажений.

Масштаб изображения на этих линиях или точках называется главным масштабом. Масштабы по другим направлениям называются частным. Размеры на искажениях на картах прямо пропорциональны размерам изображённым территориям, а в пределах 1 карты искажение увеличивается, удаление от точек или линий нулевых искажений. При проведении измерений на картах мелкого масштаба возникает необходимость учёта искажений, при этом искажения могут изменяться:

1)по таблицам;

2) по математическим формулам.

Указания по выполнению задания:

Вычислить искажения для заданной точки используя математические формулы. Задания выполняются по вариантам, которые различаются координатами точек и набором карт.

m = ₁ / L₁* M (1).

n =  ₂ / L₂  * M (2).

ε = θ - 90° (3).

p = m * n *  (4).

a + b =  (5).

a - b =  (6).

 =   (7). => w = 2 *

K =   (8).

a и b можно найти сложив почленно уравнение (5) и (6).

w = Arcsin () / 2

 - масштаб площади;

a, b – наибольший и наименьший масштаб;

w – максимальное искажение угла;

K – искажения форм для поличтения, которое необходимо измерить и вычислить следующие значения;

m – частный масштаб по параллели в долях главного масштаба;

_{1 –} длина дуги меридиана по карте ( измеряется);

_{2 –} длина дуги параллели по карте (измеряется);

L₁  - длина соответствующей дуги  меридиана на элипсойде (выбирается по таблице);

L₂  -  дуга соответствующая дуги параллели на элипсойде ( по таблице);

M – знаменатель главного масштаба, этот угол измеренный по касательной;

θ – отклонение от угла 0° на 90° .

Окончательное значение всех вычисленных величин округлять до двух знаков после запятой. Копировать на кальку рисунок с исключительной точкой.