г) возможен случай, когда перестановка отдельных элементов не приводит к уменьшению суммарной длины, хотя ее можно сократить групповой перестановкой элементов (парами, тройками и т.д.);
д) результат работы алгоритма зависит от первоначального размещения элементов в монтажном пространстве.
Для получения более точных результатов целесообразно сочетать быстрый обратный алгоритм с улучшающим размещение итерационным.
Среди итерационных алгоритмов наиболее эффективны методы, основанные на парных перестановках элементов, при этом оказывается нецелесообразным рассматривать перестановки элементов в усеченных окрестностях, что приводит к существенным сокращениям времени при той же точности результата. Алгоритмы парных перестановок позволяют уменьшить длину межсоединений от 1% до 50% в зависимости от начального размещения. Наибольшая скорость уменьшения длины соединений наблюдается на первых итерациях, монотонно уменьшаясь к значениям, близким к 1% при числе итераций К>5.
Важной характеристикой алгоритма парных перестановок является число успешных обменов среди общего числа просмотренных. Этот коэффициент минимален при использовании всех возможных n(n-1)/2 перестановок на каждой итерации и не превышает 5%. При усечении окрестности исследуемых перестановок, например, обмене лишь соседних элементов в «хорошем» начальном размещении, указанный коэффициент может достигать 50%.
Расчетная часть.
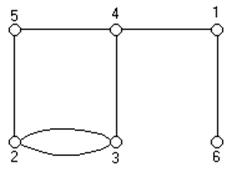
Дано монтажное пространство, в котором имеется 6 свободных позиций с центрами позиций показанной в таблице.
.
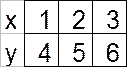
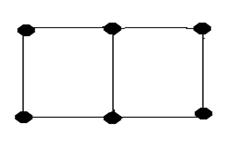
Рис 1. Монтажного пространстворис 2. Решетка графа.
 |
 |
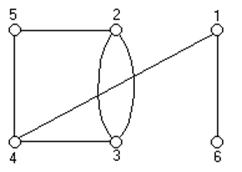
Рис. 1а Рис. 2а
Схема электрическая, принципиальная. Мультиграф схемы.
Составим матрицу расстояний D и матрицу связности R. Определим сумму элементов в каждой i-й строке матриц.

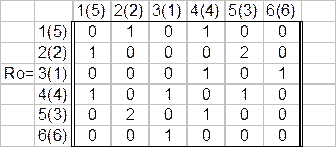
Вычислим длину соединений начального размещения
 L1=9 у.е.
L1=9 у.е.
Определим по формуле (4.5) элементы матрицы приращения:
Δl12 =2*r12*d12-[(r11-r12)(d11-d12)+(r12-r22)(d12-d22)+(r13-r23)(d13-d23)+(r14-r24)(d14-d24)+(r15-r25)(d15-d25)+(r16-r26)(d16-d26)]=0-[0*(-1)+0*1+(-2)*1+1*(-1)+(-1)*1+1*1]=0-(-3)=3 и т.д.
Δl13=2; Δl23=2; Δl14=1; Δl24=-2; Δl34=3; Δl15=0; Δl25=2; Δl35=0; Δl45=2; Δl16=3; Δl26=2; Δl36=0; Δl46=2; Δl56=4

Поскольку минимальный элемент Δl24, переставим 2-е и 4-е строки и столбцы в матрице R0, а конструктивные элементы 2-й и 4-й поменяем местами. Получим матрицу

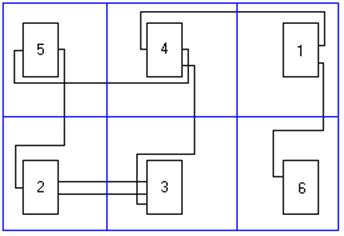
По матрице геометрии Рис. 3
Граф результата размещения.
 L2=7 у.е.
L2=7 у.е.
Снова вычислим матрицу приращения
 Рис. 4
Рис. 4
Результат размещения.
Все элементы матрицы ΔL1 положительные. Следовательно, процесс перестановки окончен, и полученный результат (рис.4) окончательный.
В этом случае алгоритм парных перестановок не дал никаких результатов:
Схема преобразована не была
L12= L21=9 у.е
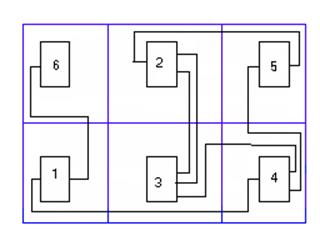
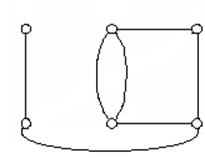
6 2 5
1 3 4
Рис. 6. Результат размещения Рис. 7 Граф результата размещения
Начальная L31= 10 у.е.
Результат работы алгоритма L31 = 8 у.е.
Вывод: с помощью алгоритма парных перестановок удалось значительно уменьшить суммарную длину соединений.
Получены следующие результаты:
- длина соединений начального размещения L1=9 у.е.
- длина соединений конечного размещения L2=7 у.е.
- суммарную длину соединений удалось уменьшить на 2 у.е.
Привет, Данил! В выводе добавь что-то типа:
С помощью алгоритм парных перестановок для алгоритма предварительного размещения результатов не дал.
С помощью алгоритм парных перестановок для алгоритма обратного размещения удалось уменьшить суммарную длину на 2 у.е.
- длина соединений начального размещения L31=10 у.е.
- длина соединений конечного размещения L32=8 у.е
Должен будешь! J
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.