Исследование эффективности алгоритмов трассировки печатных и пленочных соединений

оперативной памяти ЭВМ, необходимый для хранения информации о текущем состоянии всех ячеек коммутационного поля.

1.4.   Алгоритм Акерса

Наиболее экономичный способ кодирования состояний ячеек коммутационного поля предложен Акерсом [1 – 4]. При распространении волны ячейки поля получают отметки в соответствии с базовой последовательностью 1, 1, 2, 2, 1, 1, 2, 2, … . Данная последовательность характерна тем, что в ней любой член имеет разных соседей слева и справа. Вначале все незанятые ячейки, соседние с ячейкой-источником, помечаются 1, затем все ячейки фронта  помечаются так же 1. 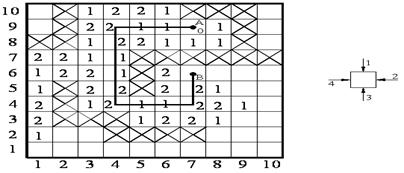Далее отметка 2 присваивается ячейкам фронта  и т. д. (рис.7.10).

Для построения пути в общем случае необходимо найти требуемую под-последовательность отметок базовой последовательности. Это легко может быть сделано по отметке ячейки-цели и отметке соседней с ней ячейки. В нашем случае цель достигнута первой 1, поэтому надо искать ячейку с отметкой 2. Их две: внизу и слева. Воспользуемся приоритетом. Вначале просматриваем ячейку снизу от цели. Поскольку ее вес равен 2, путь строим в нее. В ней вновь анализируем соседние ячейки в порядке приоритета. Ищем ячейку с весом 2. Это опять нижняя ячейка. Далее надо аналогично искать ячейку с весом 1.

Вариант соединения контактов A и B при этом заданном приоритете дан на рис.7.10.

В методе Акерса ячейка поля может находиться в следующих состояниях: пустая, занятая, иметь отметку 1 или 2. Таким образом, на каждую ячейку поля достаточно всего два двоичных разряда памяти.

1.5.   Лучевой алгоритм

Основная идея алгоритма, предложенного Л. Б. Абрайтисом [1 – 4], заключается в исследовании поля для определения пути между ячейками A и B по некоторым заранее заданным направлениям, подобным лучам. Это позволяет сократить число просматриваемых алгоритмом ячеек, а, следовательно, и время на анализ и кодировку их состояний, однако снижает вероятность нахождения пути сложной конфигурации и усложняет учет конструктивных требований к технологии печатной платы.

Рис.7.10.

Работа алгоритма заключается в следующем. Задается число лучей, распространяемых из ячейки A и B, а также порядок присвоения путевых координат. Обычно число лучей для каждой из ячеек (источников) принимают одинаковым (часто равным двум). Лучи , , …,  и , , …,  считаются одноименными, если они распространяются из одноименных источников A или B. Лучи  и  являются разноименными по отношению друг к другу. Распространение лучей происходит одновременно из обоих источников до встречи двух разноименных лучей в некоторой точке C.

Путь проводится из ячейки C, в которой встретились лучи по путевым координатам, и проходит через ячейки, по которым распространялись лучи.

При распространении луча может возникнуть ситуация, когда две соседние ячейки будут заняты. В этом случае луч считается заблокированным и его распространение прекращается.

Рассмотрим работу лучевого алгоритма на примере (рис.7.11).

Для источников A и B взято по два луча с взаимно противоположными направлениями. Поскольку разности координат  и , то для луча  допустимое направление движения вначале вниз, а в случае преграды – вправо; для луча  – вверх, влево; для  – вправо, вниз; для  – влево, вверх. Если ячейка B будет расположена не справа от A, а слева, то путевые координаты вправо и влево надо поменять местами.

На первом шаге алгоритма просматриваются ячейки с координатами (3,8), (9,3), (4,9) и (8,2). Поскольку эти ячейки оказались свободными, в них ставятся путевые координаты, которые указывают назад, т.е. на те ячейки, из которых на

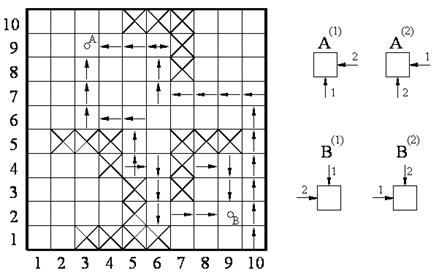
Рис.7.11.

этом шаге поступил луч. На третьем шаге луч  сверху оказывается заблокированным, поэтому он меняет направление «вверх» на направление «влево» – просматривается ячейка с координатами (8,4). На четвертом шаге луч  оказывается заблокированным, а лучи  и  встретились в ячейке C с координатами (5,4). Луч , пройдя через все поле, оказывается заблокированным в ячейке с координатами (10,1).

Путь строится из ячейки C по путевым координатам в направлении ячеек A и B. Если бы ячейка (7,2) была занята, то лучи  и  оказались бы заблокированными