Исследование эффективности алгоритма компоновки схем радиоэлектронных средств, страница 2

Коэффициент разбиения  позволяет оценивать качество разбиения графа на куски, а также сравнивать различные алгоритмы разбиения графов. Очевидно, что лучшим разбиениям для одного и того же графа соответствуют наибольшие значения .

Существует значительное количество алгоритмов компоновки, которые можно условно разбить на пять групп: 1) последовательные алгоритмы; 2) итерационные алгоритмы; 3) алгоритмы, использующие методы целочисленного программирования; 4) алгоритмы, основанные на решении задачи о назначении; 5) смешанные алгоритмы.

1.2  . Последовательные алгоритмы компоновки

Суть последовательных алгоритмов заключается в том, что вначале по определенному признаку выбирают вершину или группу вершин, к которым затем присоединяют другие вершины графа для образования первого куска. Процесс повторяют до получения заданного разбиения.

1.2.1. Метод максимальной конъюнкции – минимальной дизъюнкции

Основной критерий разбиения графа на куски – минимум числа соединяющих ребер между кусками графа. Если формировать куски  графа G так, чтобы каждый из кусков во множестве  содержал возможно большее число ребер, то при этом получится локальный минимум суммарного числа K соединяющих ребер.

Рассмотрим метод максимальной конъюнкции – минимальной дизъюнкции [1, 4].

Пусть дана схема с множеством элементов , соединенных между собой множеством электрических цепей . Ее необходимо скомпоновать в узлы, включающие по t элементов. Число внешних связей узлов не должно превышать z (z – число контактов в разъеме).

Работа начинается с формирования 1-го узла. Первым выбирается элемент, подключенный к наибольшему числу цепей. Далее последовательно оцениваются по двум параметрам возможности назначения в формируемый узел оставшихся элементов.

Вначале отбирается множество элементов, назначение каждого из которых в формируемый узел не превышает предельно допустимого числа z внешних связей узла. Затем из полученного множества элементов выбираются такие, которые имеют с назначенными в формируемый узел элементами наибольшее число общих цепей.

При работе алгоритма схема представляется в виде графа Кенига , в котором подмножество вершин E и V интерпретируют соответственно множества элементов E и электрических цепей V. При этом вершина  соединяется с вершиной  ребром  в том случае, когда элемент  принадлежит цепи . Для вычисления на ЭВМ граф  задается матрицей инцидентности , в которой число строк n определяется количеством элементов схемы, а столбцов m – количеством электрических цепей. Элемент , стоящий на пересечении i-й строки и j-го столбца, равен 1, если элемент  подключен к цепи , и нулю в противном случае.

Расчетная часть.

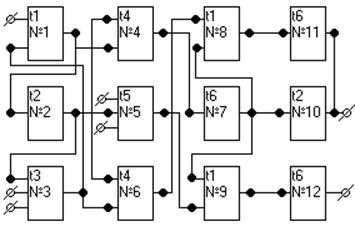
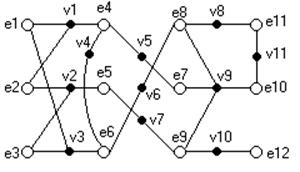
Рис.1                                                                                                              Рис.2

Принципиальная электрическая схема узла.                                                              Граф схемы.

Пусть дана схема соединений (рис.1), которую необходимо скомпоновать в узлы, содержащие не более трех элементов , и каждый узел имеет не более пяти выводов .

Граф схемы представлен на рис.2.   Q1- матрица инцидентности.

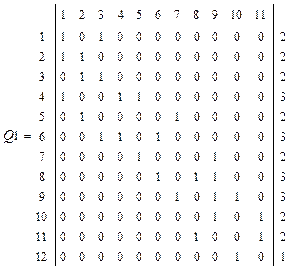
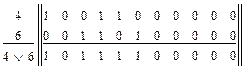Максимальную локальную степень, равную трем, имеют вершины  е4, е6, е8, е9. В качестве исходной выбираем 1-ю по порядку е4.

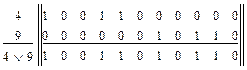
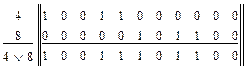
Находим суммы элементов в дизъюнкциях: c(q46)=5; c(q48)=6; c(q49)=6.

Выбираем вершины, имеющие , и включение которых в формируемый узел не превысит условия . Такой является вершина е6. Так как она единственная, то включаем ее в узел T1={e4,e6}.

Поскольку по условию в узел необходимо включить три элемента, то переходим к подбору следующей вершины.

Для этого модифицируем матрицу .

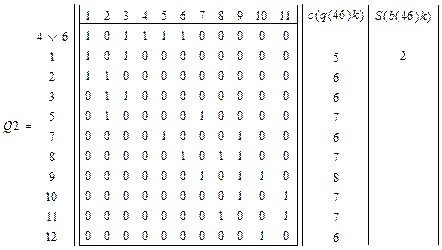
Включаем в узел элемент е1.

T= {e1, e4, e6}.

Итак, узел T1 сформирован, поскольку в него назначено три элемента. Число внешних связей у T1   .

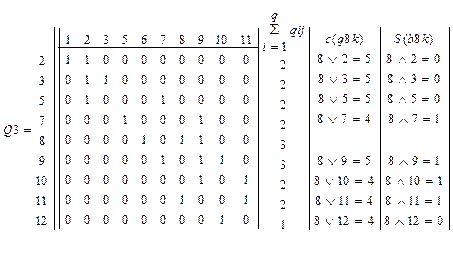Аналогично формируем второй узел T2, рассматривая оставшиеся вершины e2,e3,e5,e7,e8,e9,e10,e11,e12. Для этого из исходной матрицы Q1 исключаем строки, соответствующие элементам e1,e4,e6. Получим:

T2= {e7, e8, e11}

Т.О. , узел Т2 будет включать элементы e7,e8,e11.

Формируем второй узел T3, рассматривая оставшиеся вершины e2,e3,e5,e9,e10,e12. Для этого из матрицы Q3 исключаем строки, соответствующие элементам e7,e8,e11. Получим:

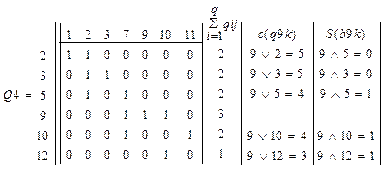
Для формирования узла Т3 выбираем элементы е9,е10,е12

Получаем: T3= {e9, e10, e12}

Оставшиеся элементы входят в оставшийся узел: T4= {e2, e3, e5}.

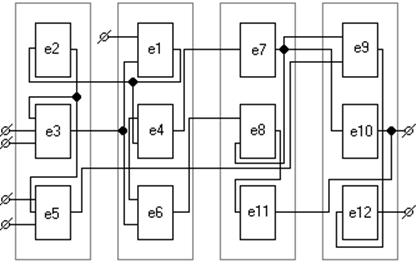
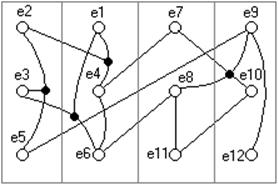
Рис.3 Преобразованный граф

Рис.4 Схема, сформированная в узлы

Условия задачи выполнены. Схема скомпонована в узлы по три элемента и число внешних соединений каждого не превышает пяти. Граф схемы, разрезанный на четыре куска, приведён на рис. 3, а схема, скомпонованная в четыре блока – на рис. 4. Качество компоновки оценим по коэффициенту разбиения DG схемы.

Общее число цепей между блоками , число цепей внутри блоков .

Тогда коэффициент разбиения схемы .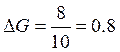

Выводы

Достоинствами последовательных алгоритмов компоновки по связанности являются их простота реализации на ЭВМ и высокое быстродействие. Кроме этого, они позволяют легко учитывать дополнительные ограничения на компоновку: несовместимость отдельных элементов в узле, априорно заданное функциональное распределение некоторых элементов схемы и др.

Недостатком этих алгоритмов является локальный пошаговый характер оптимизации, приводящий к тому, что в начале процесса выделяются сильно связанные группы элементов, в то время как в последние узлы попадают мало связанные или вообще не связанные элементы. При жестких ограничениях на число выводов это приводит к увеличению числа узлов.

Поэтому эффективность таких алгоритмов выше при компоновке узлов с небольшим отношением числа элементов к числу выводов (печатных плат, панелей и т. д.). Кроме этого, результаты лучше для схем с относительно невысокой связанностью.