Исследование эффективности алгоритмов трассировки проводных соединений

ищется вершина, ближайшая от всего построенного фрагмента дерева. Отсюда, в отличие от алгоритма Краскала, единственное строящееся поддерево последовательно наращивается до построения остова.

Основные принципы построения минимального связывающего дерева (или кратчайшей связывающей сети) при наличии ограничений на локальные степени вершин  следующие.

В начале любая произвольная вершина  соединяется с ближайшей соседней, образуя исходное поддерево. (Для определенности построения минимального дерева можно начинать с ребра, инцидентного первой вершине , или с минимального ребра). На каждом последующем шаге к строящемуся поддереву присоединяют очередное ребро минимально возможной длины, связывающее новую, еще не присоединенную вершину  с одной из вершин поддеревьев , локальная степень которой .

Для реализации алгоритма составляют матрицу расстояний , элемент  которой вычисляют по одной из формул (5.1) или (5.2). Просматривают элементы первой строки матрицы D и находят минимальный элемент. Пусть таким оказался элемент g-го столбца, тогда весь 1-й и g-й столбцы матрицы D исключаются из рассмотрения, а первое соединение проводится между точками  и . Просматриваются 1-я и g-я строки матрицы с оставшимися элементами. Из элементов этих строк находится минимальный. Предположим, что им оказался элемент, принадлежащий j-му столбцу. Если этот элемент находится на пересечении с первой строкой, то точку  соединяем с 1-й точкой (), если же он находится на пересечении с g-й строкой, то точку  соединяем с g-й (), после чего из матрицы D исключаем все элементы j-го столбца. Просматриваются 1-я, g-я и j-я строки и т. д.

Выполнение ограничения на локальную степень  вершин обеспечивается проверкой в каждой просматриваемой  i-ой строке числа уже выбранных для построения минимального дерева элементов – . При  все оставшиеся элементы i-й строки исключаются из рассмотрения, т.е. эта строка удаляется.

АЛГОРИТМ

1. Вычислить элементы матрицы расстояний  по одной из формул – (5.1) или (5.2).

2. Найти минимальный элемент матрицы , где ; . Номера строки и столбца q и p, на пересечении которых он находится, определяют номера вершин  и , соединяемых ребром.

3. Занести номера вершин во множество , построенное ребро – во множество .

4. Подсчитать локальные степени  и , подлежащих соединению на данном шаге вершин  и .

5. Проверить условие  и . Индексы вершин, для которых это условие не выполняется, указывают номера строк матрицы D, которые необходимо исключить из рассмотрения.

6. Найти . Здесь , , т. е. среди еще не вошедших в дерево вершин отыскать вершину , минимально удаленную от некоторой вершины дерева .

7. Дополнить множества ; .

8. Проверить, все ли вершины графа соединены ветвями . Если условие выполняется, идти к 9, иначе – к 4.

Конец.

Расчетная часть.

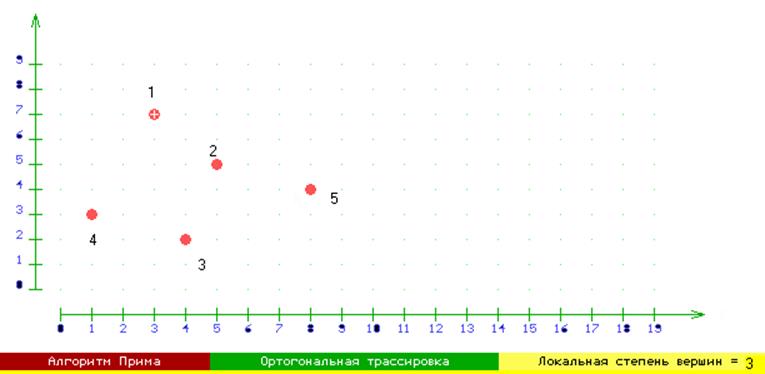
Рис. 3.

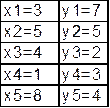
Составляем матрицу длин:

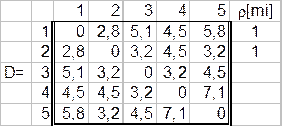
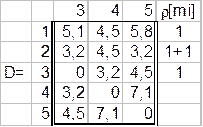
Просматриваем все строки матрицы и выбираем элемент, являющийся минимальным. Помечаем его, локальные степени 1-й и 2-й вершин увеличиваем на единицу. Исключаем из рассмотрения (вычеркиваем) все элементы первого и второго столбцов. Соединяем m1 и m2.

Просматриваем вторую и  третью строки матрицы. Выбираем элемент d23=3,2; локальные степени 2-й и 3-й вершин увеличиваем на единицу.

Исключаем из рассмотрения элементы 3-го столбца. Соединяем m2 и m3.

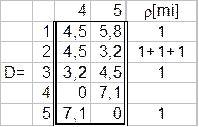
Просматриваем вторую и третью строки матрицы. Выбираем элемент d25=3.2; локальные степени 2-й и 5-й вершин увеличиваем на единицу.

Исключаем из рассмотрения элементы 5-го столбца и 2-й строки (к 2-й вершине m подключено уже три ребра).

Соединяем m2 и m5.

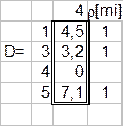
Просматриваем первую и третью строки матрицы. Выбираем элемент d34=3.2. Соединяем m3 и m4.

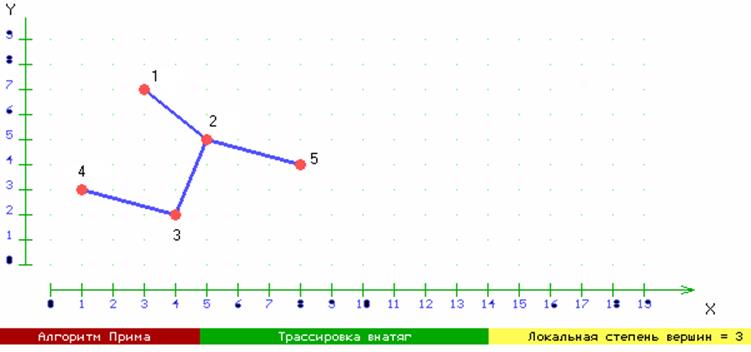
Рис. 4.

Минимальное связывающее дерево, полученное в результате решения, приведено на рис.4

Множество ребер в нем R={r12, r23, r25, r34}=4=(n-1). Суммарная длина его ребер L равна 12.4

Вывод: Для обоих алгоритмов получили одинаковые графики и суммарную длина его ребер L=25

Оба рассмотренных алгоритма позволяют при выполнении соответствующих