Исследование эффективности алгоритма покрытия схем модулями (Лабораторная работа № 1), страница 2

где а_к – число элементов в модуле T_k; b_k – число элементов типа k в схеме; { } – символ ближайшего большого целого; x_k – число использованных модулей типа k. Отметим, что для модулей с однотипными элементами получаем квадратную матрицу , причем  a_k = 0 при , и .

б) Практический интерес представляют наборы модулей с разнотипными элементами.

Пусть известны:

1) Библиотека типовых элементов, содержащая m типов интегральный микросхем (ИМС). Общее число типов элементов в ИМС библиотеки l. Тогда библиотеку зададим матрицей вида .

2) Электрическая схема узла, состоящая из соединения элементов одинаковых типов. Зададим схему вектором .

АЛГОРИТМ  1

1. Составить вектор  количественного состава схемы по типам элементов: .

2. Упорядочить модули (микросхемы) T_k библиотеки по возрастанию их стоимостей:

 .

3. Составить матрицу  описания состава библиотеки в соответствии с их стоимостью; .

4. Выполнить поэлементное деление вектора  на строку  матрицы A:

 для , .

5. Найти  и на данном шаге использовать  модулей типа k.

6. Найти вектор непокрытых элементов

, где ; .

7. Если элементы , перейти к , если , перейти к .

8. Определить количество использованных ячеек каждого типа

 ( – определяет число итераций) и вычислить их суммарную стоимость: .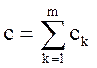

Конец.

ПРИМЕР 1.1

Пусть дана электрическая схема (рис.1.1), которая состоит из элементов типа t₁, t₂, t₃, и t₄ (рис.1.2). Существует библиотека ИМС  (рис.1.3), причем их условные стоимости равны соответственно: ; ; ; ;  условных единиц стоимости.

Требуется выполнить покрытие с минимальной стоимостью схемы на рис.1.1 набором микросхем из библиотеки рис.1.3.

Решение

Сосчитаем количество элементов каждого типа в схеме: , , ,  и составим вектор количественного состава: .

Для покрытия выберем микросхемы  как наиболее дешевые.  В необходимый набор не включаем, поскольку два  из трех ее элементов реализуют функцию, которая отсутствует в схеме рис.1.1.

Упорядочим выбранные ИМС по возрастанию их стоимостей: T₁, T₂, T₃ .

Составим матрицу описания состава ИМС библиотеки с учетом их стоимостей:

.

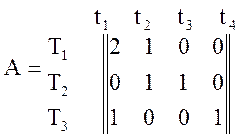Выполним поэлементное деление вектора  на строку  матрицы A. В делении участвуют только значащие числа, а в результатах делений учитываются только целые части

.

В результате для ИМС  имеем , .

Берем min из значащих чисел {2, 4}: . Следовательно, для покрытия схемы назначаем 2 шт. ИМС . Формируем строку .

Находим вектор непокрытых элементов . Для этого из вектора  поэлементно вычитаем удвоенную строку –

 .

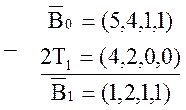Далее выполним аналогичные действия для ИМС , стоимость которой .

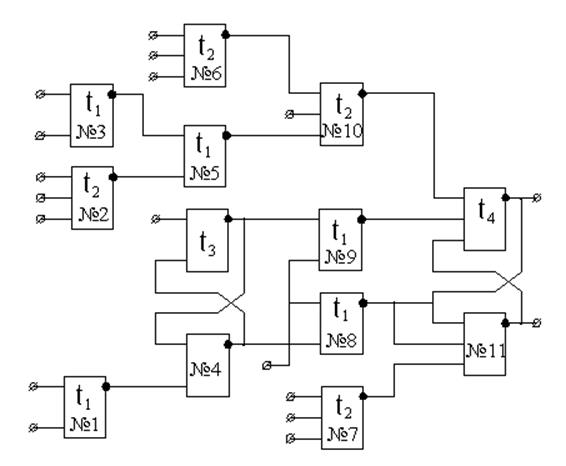
Рис. 1.1

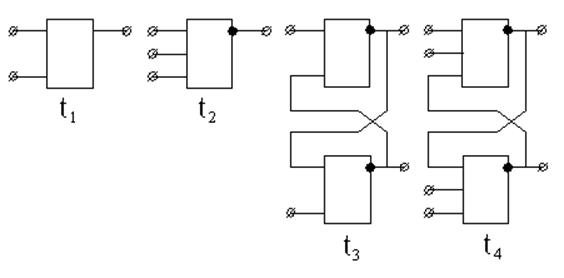
Рис. 1.2

Рис. 1.3

Вектор  поделим поэлементно на строку :

.

Значащими в результате деления будут ,. Минимум из них  , поэтому для покрытия схемы назначаем 1 шт. .

Определяем вектор непокрытых элементов :

  .

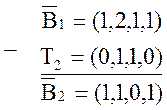Произведем покрытия оставшихся элементов ИМС , так как . Поделим вектор  поэлементно на строку :

.

Поскольку ,, получим , и для покрытия схемы назначаем 1шт. .

Вектор непокрытых элементов  будет:

 .

Поскольку , вновь выполним покрытие самой дешевой ИМС . Поделим  на строку :

.

. Назначаем еще 1 шт. . Вектор непокрытых элементов :

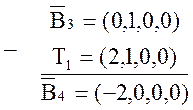
Наличие отрицательного элемента (-2) в  указывает на избыточность двух элементов  в покрывающих ИМС. Итак, процесс покрытия закончен. В итоге получили 3 шт. , 1 шт.  и 1 шт. . Коэффициент покрытия схемы G = 11/5 = 2,2.

Результаты расчетов сведены в табл.1.1. В скобках указано число элементов (по типам) в исходной схеме рис.1.1.

Таблица 1.1