Условия образования твердых растворов и фаз внедрения (специальных карбидов, нитридов) в сплавах на основе железа. Магнитомягкие материалы, их состав, свойства, области применения, страница 6

Емкостной дилатометр. Емкостной дилатометр основан на изменении емкости конденсатора, одна из пластин которого связана с исследуемым образцом и смещается при его удлинении. Это приводит к изменению емкости конденсатора, последнюю измеряют путем подстройки всего контура. Емкостной метод был применен для измерения удлинения  при низких температурах. Относительная ошибка составляет 5 %.

Интерференционный дилатометр. В основу прибора положен интерферометр Линника. В интерферометр входит микроскоп, между объективом которого и окуляром помещена призма. На уровне призмы расположен объектив с зеркалом, напротив объектива помещается источник монохроматического света. Образец, находящийся в кварцевой трубке, помещен в печь, которая прикреплена к основанию корпуса прибора. Интерференция возникает вследствие оптической разности хода двух лучей, появляющихся при разложении света призмой. Часть лучей проходит через призму, отражается зеркалом и, попадая опять в призму, отражается в направлении окуляра. Другую часть лучей призма отражает на зеркало и от него в окуляр. Перемещение образца вызывает смещение зеркала, и интерференционная картина изменяется.

Дилатометр Стрелкова. Дилатометр Стрелкова основан на преобразовании поступательного движения образца, вызванного термическим расширением, во вращательное движение, которое измеряется с помощью автоколлимационных труб с окуляр-микрометрами. Дилатометр предназначен для измерения удлинения (сжатия) при температурах от комнатной до 1000ºС. По чувствительности он близок к интерференционному, мало чувствителен к вибрациям.

Общим недостатком описанных приборов является использование кварца для опор и передающих расширение образца стержней и трубок.

Кварц деформируется при 1000—1100° С, и эти температуры являются предельными для точных измерений с помощью большинства приборов.

Разработан прибор, позволяющий производить определение коэффициента расширения до 2400°С. С помощью оптического компаратора наблюдается и фиксируется перемещение верхнего конца испытуемого образца. До 1000°С конец образца освещается наружным источником света, с 1000° С достаточна собственная радиация испытуемого образца. Нагрев образцов производится в угольной печи сопротивления, в атмосфере аргона.

Из зависимости потенциальной энергии взаимодействия атомов в решетке U, межатомного расстояния r (рис. 1) видно, что изменение межатомного расстояния с ростом температуры (термическое расширение) будет наблюдаться только при несимметричной зависимости U (r) (см. рис. 1, сплошная кривая). С ростом температуры энергия взаимодействия U повышается и центр колебаний атома (r₀) смещается в сторону больших r. Для получения аналитической зависимости α от температуры необходимо воспользоваться таким соотношением для потенциальной энергии атома, которое отражало бы ее асимметричный характер при смещении атома из положения равновесия: U(x)=аx²—bx³, где а — коэффициент, характеризующий гармоническую связь; b — коэффициент, характеризующий ангармоническую связь; х — смещение атома из положения равновесия; r=r₀+х.

При экспериментальном определении коэффициент термического расширения получают из соотношения =[l+(Т₂—Т₁)], где ,— длины образца при температурах Т₂ и Т₁, -средний коэфф расширения

Отсюда  

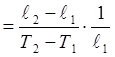
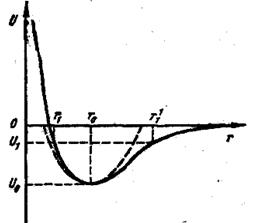
Рас. 1. Зависимость энергии взаимодействия атомов от расстояния между ними

При переходе к истинному коэффициенту расширения разности Т₂—Т₁ и - стремятся к нулю, а длина  к  (длина при температуре Т). Истинный коэффициент 

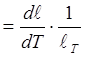
Экспериментальную зависимость длины  от температуры Т обычно описывают с помощью степенного ряда

= (1 + αt + α′t²+...), при α, α′... постоянные величины;  — исходная длина при температуре Т₀, t = Т — Т₀.

α_Т= α_р+ α_э+ α_м

где α_р, α_э, α_м...—коэффициенты, характеризующие вклад колебаний кристаллической решетки, энергии электронов, магнитного взаимодействия и другие вклады.

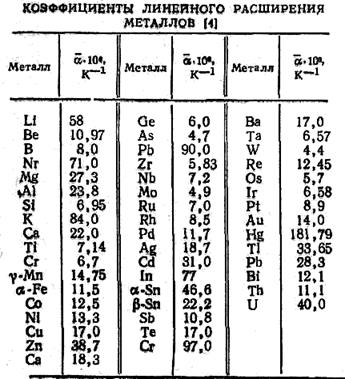
Средний коэффициент линейного расширения () металлов для интервала температур 0—100 °С приведен в табл. 1.

Для металлов с кубической решеткой величина α_Т практически не зависит от кристаллографического направления. Для некубических кристаллов эта зависимость значительна.

При образовании твердых растворов металлов коэффициент термического расширения линейно зависит от количества второго компонента. В случае твердого раствора на базе переходных металлов значение α_Т ниже, чем определяемое по правилу аддитивности.