Жидкое состояние. Гомогенная кристаллизация, страница 7

Конечной целью любой теории жидкостей является получение соотношений, позволяющих описать область  их существования, объяснить поведение различных равновесных и кинетических   характеристик на основе знания свойств отдельных атомов или молекул, их взаимного расположения, законов передвижения и взаимодействия. Любая жидкость представляет собой систему из огромного числа взаимодействующих друг с другом частиц.   Следовательно,   задачи, теории жидкого состояния составляют предмет исследования статистической физики и могут быть решены только методами   статистической физики.

Ранние попытки создания теории простых одноатомных жидкостей исходили из представления о жидкостях, как о кристаллах со значительными нарушениями порядка, возникающими в результате образования вакантных узлов (дырок) в кристаллической решетке. Предполагалось, что наличие дырок облегчает возникновение новых дырок. С увеличением температуры этот процесс образования вакансий должен был идти с нарастающей скоростью, лавинообразно и приводить к полному исчезновению регулярной структуры. Этот момент интерпретировался как фазовый переход кристалл—жидкость. Грубо говоря, плавление наступало тогда, когда из кристаллической решетки изымалось такое количество атомов, что оставшийся симметрично построенный каркас рушился, порядок в расположении атомов исчезал. Сейчас известно, что в твердых металлах вблизи температуры плавления концентрация вакансий не превышает 0,1% и, таким образом, в ближайшее окружение вакансии входят ионы решетки, а не дырки. В этом случае малообоснованным является предположение об уменьшении энергии образования вакансий при увеличении их числа. Такое предположение было бы оправдано, если бы вакансии располагались рядом друг с другом.

У большинства веществ, составленных из сферических плотноупакованных частиц, в точке плавления происходит скачкообразное изменение объема. При температуре плавления моль жидкости, находящийся в равновесии с кристаллом, занимает больший объем, чем моль соответствующего кристалла.

Этот дополнительный «свободный объем» лег в основу нескольких вариантов теории жидкостей, также тесно связанных своими идеями с квазирешеточными теориями.

Использование методов статистической физики в первых решеточных моделях жидкостей дало возможность получить простейшие уравнения состояния жидкостей, выражения для термодинамических свойств фазы: свободной энергии, энтропии и некоторых других равновесных свойств, например сжимаемости.

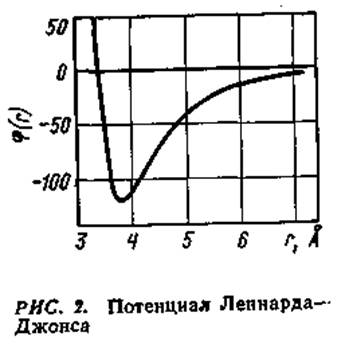
В ячеечной теории жидкости объем, занимаемый жидкой фазой, разбивается на ячейки, число которых считается равным числу молекул N. Движение молекулы в каждой ячейке рассматривается как движение в усредненном поле сил взаимодействия со всеми остальными молекулами в свободном объеме, который представлен данной молекуле ее Zближайшими соседями. Предполагается, что потенциал взаимодействия с остальными молекулами быстро убывает с увеличением расстояния; обычно ограничиваются взаимодействием молекулы с ближайшими соседями. Преимущественно используется потенциал Леннарда — Джонса (рис. 2)

где е и а — постоянные величины.

Первое слагаемое в скобках описывает уменьшение сил отталкивания с расстоянием, второе — увеличение   сил   притяжения.   Силы притяжения, как и энергию притяжения, принято считать отрицательными.

Величина а равна эффективному диаметру частицы жидкости (при r=a, f(r)=f(a)=0, рис. 1). Величина 8 определяет глубину потенциальной ямы и характеризует молекулярное поле, созданное в месте нахождения молекулы ее соседями, т. е. характеризует интенсивность межмолекулярных сил.

В приближении быстроубывающего с увеличением расстояния потенциала внутренняя энергия жидкости равна сумме парных потенциалов взаимодействия, а свободная энергия F оказывается равной

ф(0)— значение   среднего   потенциала   взаимодействия   в   центре яч'ейки;