ставка сложная, то для решения задачи воспользуемся функцией КПЕР (см. строку 2 в табл. 3).
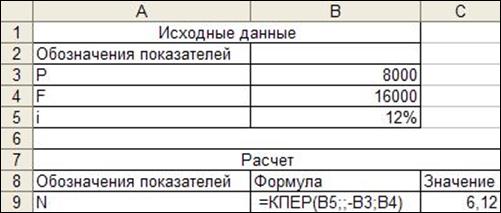
Рис. 6. Расчет срока платежа
5.2. Определение ставки процента
Задача 3. Определить величину сложной ставки процента, при которой сумма 5000 руб. утроится за 4 года. Для решения задачи воспользуемся функцией СТАВКА из табл. 4.
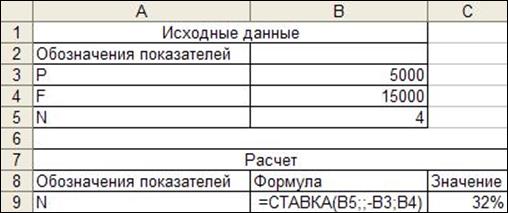
Рис. 7. Расчет сложной ставки процента
6.1. Расчет дисконтированной суммы
Задача 4. Имеется финансовый инструмент 10000 руб. со сроком погашения через два года. Какую сумму получит владелец, если учтет его в банке по сложной учетной ставке 15%? Какова величина дисконта D?
Для решения задачи воспользуемся функцией ПС (см. строку 6 табл. 2).
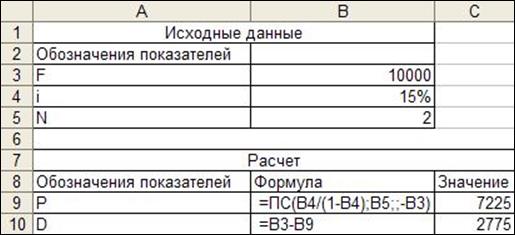
Рис. 8. Расчет дисконтированной суммы
6.2. Сравнение роста по сложной ставке процента и учетной сложной ставке процента
Сравним скорость роста по сложной ставке процента и учетной сложной ставке. Воспользуемся условием задачи из п.6.1. Пусть имеется долговое обязательство 7225. Сравнить скорость роста по простой и учетной ставке 15%.
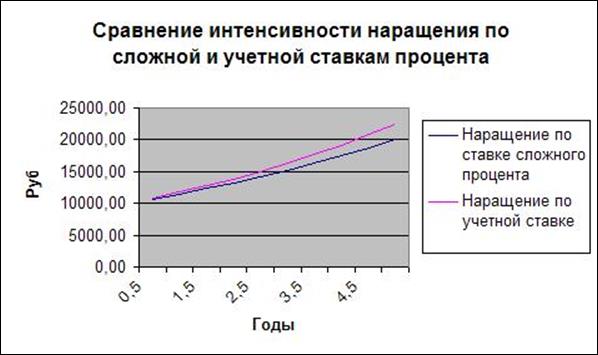
Рис. 9. Сравнение интенсивности наращения по сложной и учетной ставкам процента
Из графика видно, что процесс наращения по учетной ставке идет более интенсивно.
7.1. Непрерывное наращение процентов
Задача 5. На сумму 200000 руб. начисляются проценты из расчета 10% в год непрерывно. Определить наращенную сумму через 4 года.
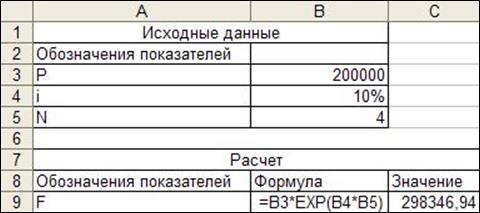
Рис. 10. Расчет наращенной суммы
7.2. Расчет силы роста
Задача 6. Имеется финансовое обязательство в 5000 руб., которое должно быть погашено через 3 года в размере 6000 руб. Определить силу роста, если проценты начисляются непрерывно.
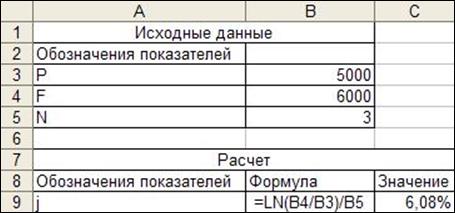
Рис. 11. Расчет силы роста
На практике часто возникают задачи по замене одних платежей другими, отличающимися сроками, ставками, способами начисления процентов. В этих случаях возникает проблема определения принципа, на основе которого производится замена. Общепринятым принципом является финансовая эквивалентность обязательств.
Выделяются следующие задачи, связанные с соблюдением финансовой эквивалентности обязательств:
8.1. Финансовая эквивалентность платежей
Эквивалентными считаются платежи, которые при приведении к некоторому моменту времени оказываются равными.
Задача 7. Имеются два платежа, первый платеж выплата 100 000 руб. через 2 года и 120 000 руб. через 3 года при условии, что проценты начисляются по сложной ставке 12% в год.
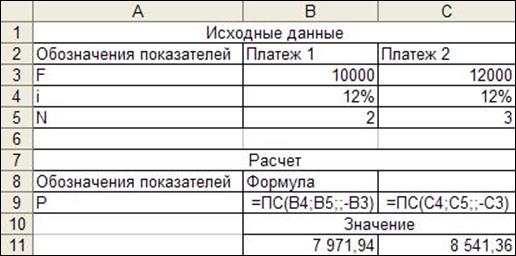
Рис. 12. Расчет финансовой эквивалентности платежей
Следовательно, платежи не эквивалентны: дисконтированная стоимость первого платежа меньше, чем у второго.
8.2. Эквивалентность процентных ставок
Иногда возникают задачи по замене одного способа начисления процентов другим при обеспечении эквивалентности платежей.
Для решения таких задач используют так называемые формулы эквивалентности, которые определяются путем преобразования равенства двух множителей наращивания. Например, для замены сложной ставки процента с капитализацией m раз в год на простую ставку процента в результате преобразования равенства двух множителей наращения (формулы 3 и 8) получим следующую формулу эквивалентности:
(1 + j / m) N * m - 1
i = ─────────── (19)
N
Для решения этой задачи на табличном процессоре нет необходимости выводить формулу эквивалентности.
Задача 8. Какой простой ставкой можно заменить сложную ставку 20% в год с поквартальной капитализацией, если сумма в 200000 рублей выдана на 5 лет.
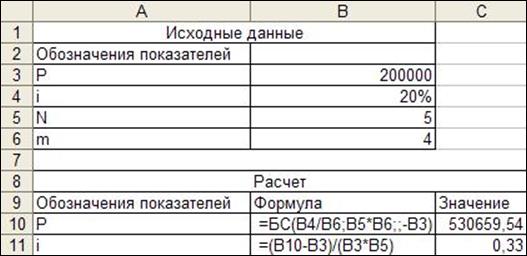
Рис. 13. Расчет эквивалентной ставки
Следовательно, эквивалентная простая ставка составляет 33%.
8.3. Расчет номинальной и эффективной ставки
В финансовых договорах могут предусматриваться различные варианты начисления процентов. Для сравнения доходности вариантов начисления процентов используется понятие эффективная ставка. Под эффективной ставкой подразумевается годовая ставка сложных процентов с капитализацией процентов раз в год. Расчет эффективной ставки процента можно проводить за два шага: на первом шаге определить наращенную или современную сумму, на втором шаге применить функцию СТАВКА. Однако в табличных процессорах существует более простой способ расчета – функция ЭФФЕКТ, которая по заданной номинальной ставке определяет эффективную ставку. В составе финансовых функций имеется и обратная функция НОМИНАЛ.
Задача 9. Имеется два вклада, первый вклад в размере 500 000 руб. внесен сроком на 4 года при условии поквартального начислением процентов по сложной годовой ставке 12%. Второй вклад в размере 600 000 руб. внесен на 5 лет при сложной годовой ставке 12,4% с полугодовым начислением процентов. Какой из вариантов более доходный?
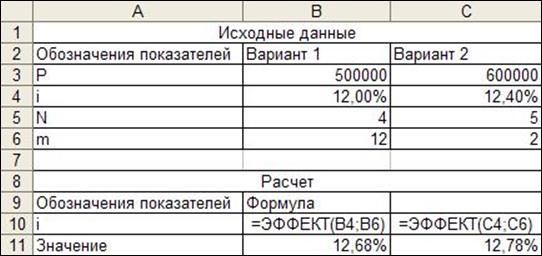
Рис. 14. Расчет эффективной ставки
Расчеты показывают, что второй вариант доходнее.
8.4. Расчет средних процентных ставок
Иногда в финансовых задачах возникает необходимость замены
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.