Интенсификация теплоотдачи при кипении

3. ИНТЕНСИФИКАЦИЯ ТЕПЛООТДАЧИ ПРИ КИПЕНИИ

3.1. ИНТЕНСИФИКАЦИЯ ТЕПЛООТДАЧИ ПРИ КИПЕНИИ

В БОЛЬШОМ ОБЪЕМЕ

Интенсивность теплоотдачи при кипении существенно зависит от режима теплосъема и при пленочном кипении она резко понижается. Поэтому интенсификация теплоотдачи при кипении также имеет большое значение.

Основная характеристика теплоотдачи при кипении

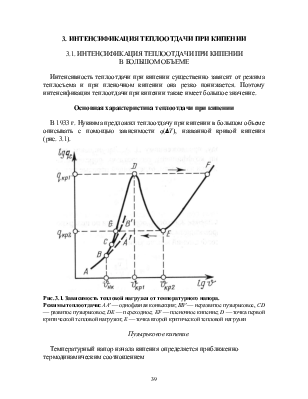
В 1933 г. Нукияма предложил теплоотдачу при кипении в большом объеме описывать с помощью зависимости q(DT), названной кривой кипения       (рис. 3.1).

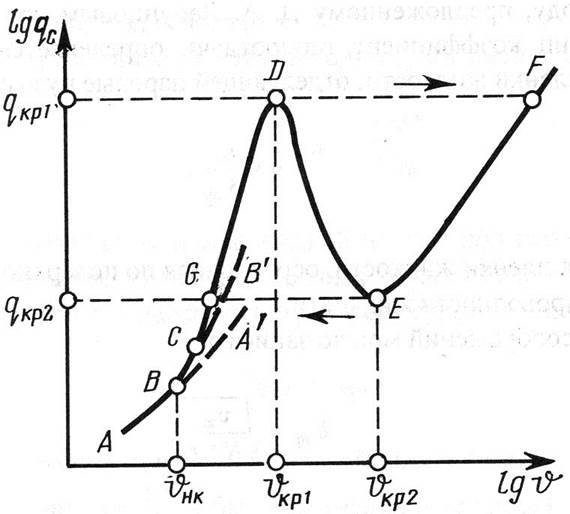Рис. 3.1. Зависимость тепловой нагрузки от температурного напора.

Режимы теплоотдачи: АА' ¾ однофазная конвекция; ВВ' ¾ неразвитое пузырьковое, CD ¾ развитое пузырьковое; DE ¾ переходное; EF ¾ пленочное кипение; D ¾ точка первой критической тепловой нагрузки; E ¾ точка второй критической тепловой нагрузки

Пузырьковое кипение

Температурный напор начала кипения определяется приближенно термодинамическим соотношением

где R_кр ¾ критический радиус парового зародыша; s ¾ коэффициент поверхностного натяжения; T_s¾ температура насыщения; r ¾ теплота парообразования; ρ_п ¾ плотность пара.

Чтобы уменьшить температурный напор начала кипения, на поверхности нагрева следует создать благоприятные условия для возникновения и развития паровых пузырей.

При пузырьковом кипении тепловой поток  передается за счет конвекции в жидкости на участках поверхности между паровыми пузырями и испарения на участках поверхности, контактирующих с пузырями. При небольших  тепловой поток передается, в основном, за счет конвекции в жидкости. При q_с, близких к q_кр1, доля теплового потока, передаваемого паровыми пузырями, становится преобладающей.

Согласно подходу, предложенному Д. А. Лабунцовым, при развитом пузырьковом кипении коэффициент теплоотдачи определяется термическим сопротивлением пленки жидкости, отделяющей паровые пузыри от стенки

где d_эф ¾ толщина пленки жидкости, осредненная по поверхности; l_ж ¾ коэффициент теплопроводности жидкости.

Из физических соображений можно записать

где n_ж ¾ коэффициент кинематической вязкости жидкости; f ¾  частота отрыва паровых пузырей,  ¾ относительная плотность центров парообразования:

где  ¾ максимальный диаметр впадины на данной поверхности;  ¾ критический диаметр парового зародыша.

Величину f можно определить как

где w ¾ средняя скорость парообразования.

Кризис теплообмена

При достижении q_кр1 начинает развиваться кризис теплообмена. Для объяснения этого явления существует несколько гипотез. Среди них наибольшее распространение получила гидродинамическая модель кризиса теплообмена, разработанная  С.С. Кутателадзе и Н. Зубром.

Согласно тепловой модели, разработанной В.В. Яговым, кризис теплообмена возникает  вследствие того, что диаметр сухого пятна под паровым пузырем достигает критической величины l_кр, пропорциональной предотрывному размеру парового конгломерата.

Тепловая нагрузка, приходящаяся на одно сухое пятно, записывается как

где  ¾ эффективная толщина жидкой пленки под паровыми конгломератами; С ¾ постоянная. Условием кризиса теплообмена считается равенство тепловой нагрузки на испарение по границам сухого пятна средней тепловой нагрузке:

.

Это обосновывается тем, что с дальнейшим ростом q происходит резкое уменьшение отношения  и быстрое увеличение площади сухих пятен.

Переходный режим кипения

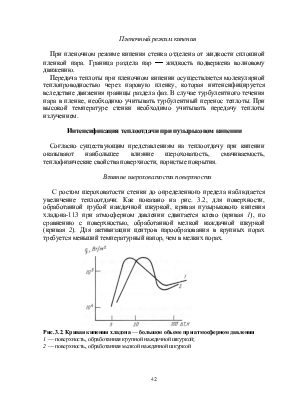
При переходном режиме кипения поверхность попеременно контактирует с паром и жидкостью. Относительная площадь и продолжительность контакта стенки с паром с ростом DТ постепенно увеличивается