Охлаждение нагретых тел в наножидкостях, страница 5

Представим это воздействие в виде графика, по оси ординат которого будет откладываться безразмерный параметр:    

По оси ординат будем откладывать безразмерную плотность теплового потока:  

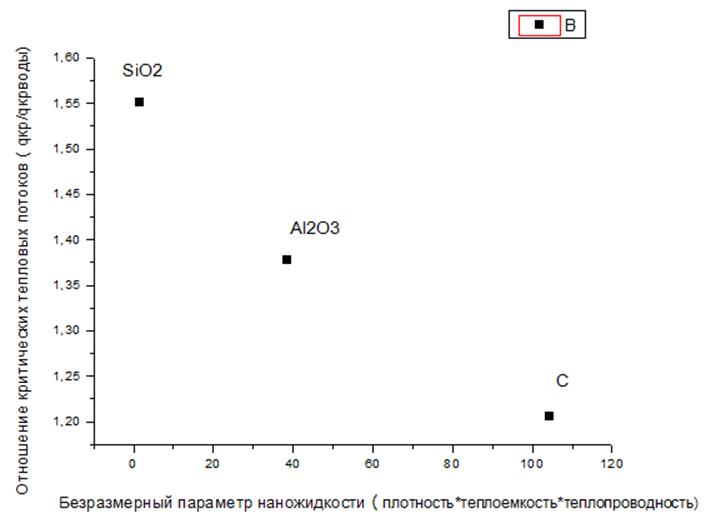
Рис.16. Характерные точки для критического теплового потока и безразмерного параметра, характеризующего теплофизические свойства наножидкостей.

Теперь попробуем описать полученные точки некой функцией.       

В итоге подбора, получили формулу, которая выглядит следующим образом: 

На рисунке ! кривая, описывающая эту формулу показана тонкой сплошной линией.

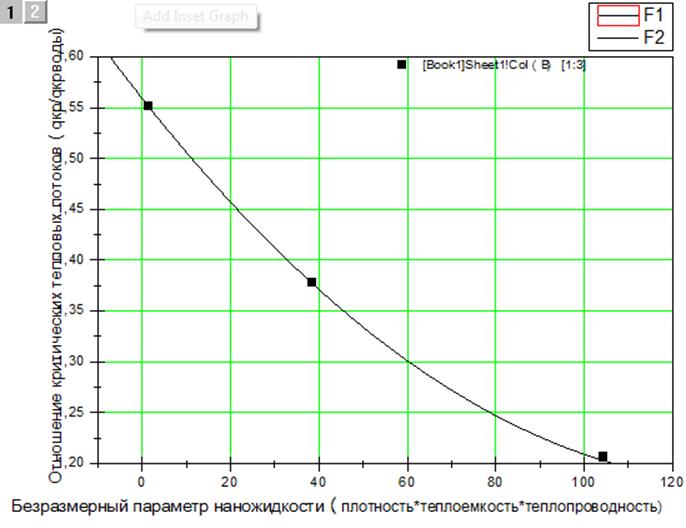
Рис.17. Зависимость безразмерного критического теплового потока от от безразмерного параметра наножидкости.

2.2. Влияние смачиваемости наножидкости на критическую плотность теплового потока

Приведем, еще раз, график, полученный H. Kim, G. DeWitt и др. пказывающий уровень краевого угла для различных наножидкостей.

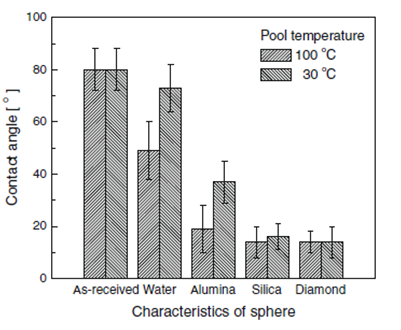
Рис.18. Краевой угол для чистой воды непосредственно после выращивания  и охлаждения SS сфер в воде и наножидкости [3]

Попробуем представить влияние краевого угла на величину критического теплового потока. Опять же, представим это влияние в виде графика. По осям ординат будет откладываться безразмерный параметр:  , где - краевой угол наножидкости,- краевой угол воды (значения берутся в работе [1]).

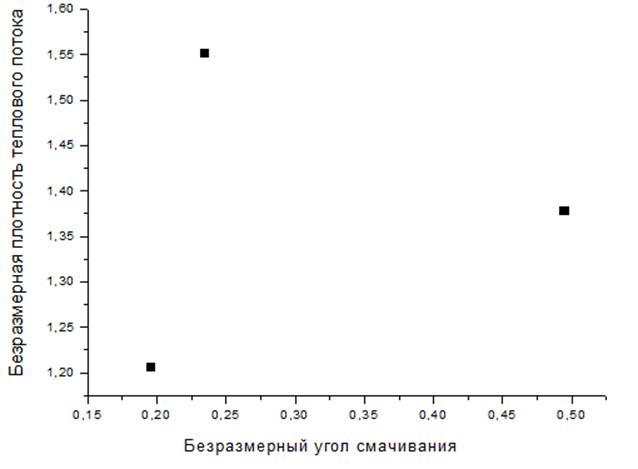
Рис. 19.Характерные точки для безразмерного критического теплового потока и безразмерного угла смачивания.

Опять же, попробуем описать полученные точки некой функцией.

В результате подбора, получилась функция вида: 

График этой функции показан на рисунке ниже тонкой сплошной линией.

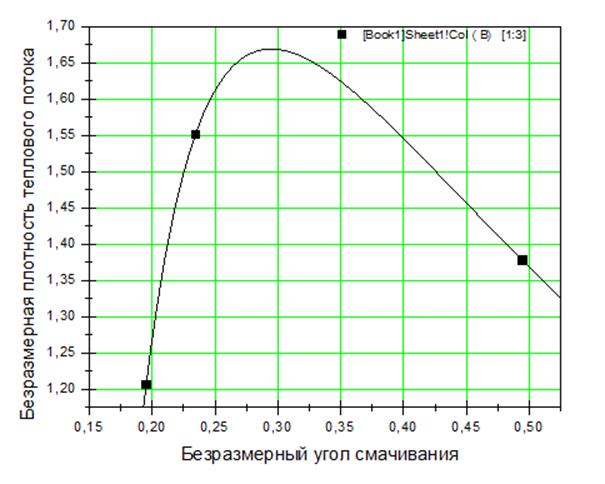
Рис. 20.Зависимость  безразмерного критического теплового потока и безразмерного угла смачивания.

Рассмотрев влияние 2-х безразмерных параметров, попробуем составить зависимость, которая будет учитывать оба этих параметра. Теперь в качестве параметра, откладываемого по оси абсцисс, будет выступать безразмерный параметр вида:

По оси ординат будет все так же выступать безразмерный параметр теплового потока.

В итоге, получим график  следующего вида (см. рис !)

Точками показаны экспериментальные данные по работе [1]. Тонкой сплошной линией указана подобранная нами формула. Она имеет следующий вид: 

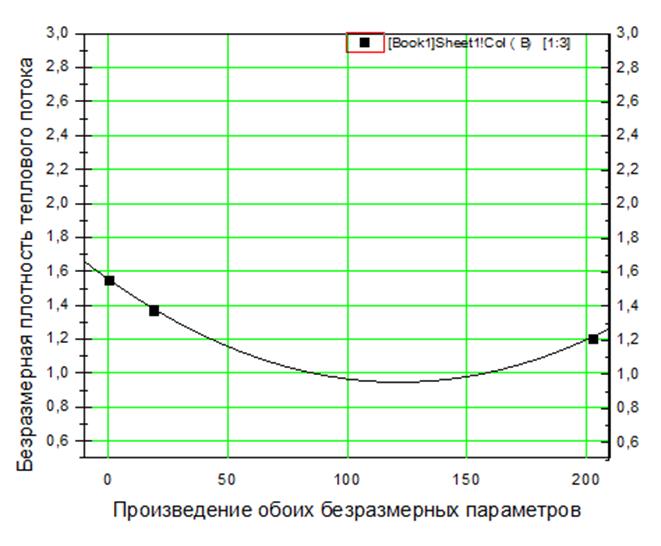
Рис.21. Характерная зависимость безразмерного критического теплового потока от произведения двух вышеизложенных безразмерных параметров.

Итак, в ходе работы мы получили формулу вида:

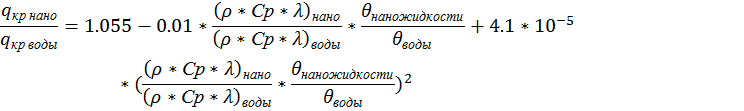
Найдем  по формуле Ягова. Так как эксперименты по работе [1] проводились при атмосферном давлении, то формула будет выглядеть следующим образом:

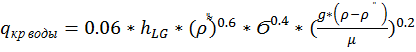, где

- удельная теплота парообразования, - плотность воды при 100 ^оС,

- плотность водяного пара при 100 ^оС, -поверхностное натяжение, - динамическая вязкость, -ускорение свободного падения

Итак, сопоставим результаты, полученные с помощью вышеизложенной формулы, с теми, что получены в экспериментах: 

Представим это на графиках (черным крестиком показаны результаты, полученные с помощью нашей формулы):

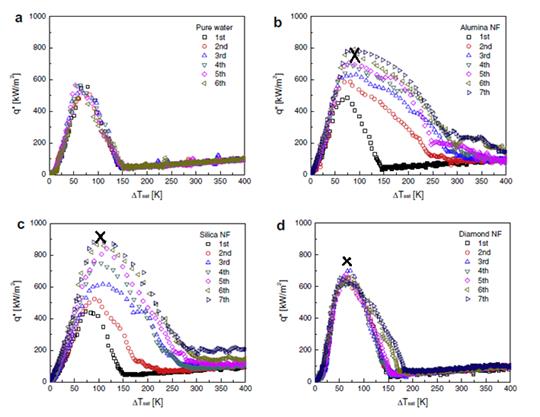
Рис. 22. Сопоставление критических плотностей тепловых потоков, полученных в эксперименте [1] с критическими плотностями тепловых потоков, полученных по нашей формуле.

Выводы

1.  В ходе работы, нами было исследовано ряд работ, посвященных охлаждению перегретых тел в жидкости. Особое внимание было уделено работе [1].

2.  Получена зависимость безразмерного критического теплового потока от безразмерного параметра, характеризующего теплофизические свойства наножидкости.

3.  Получена формула, с помощью которой можно определить значение критического теплового потока в зависимости от угла смачиваемости и теплофизических свойств жидкости.

Список литературы

1.  Hyungdae Kim, Gregory DeWitt, Thomas McKrell, Jacopo Buongiorno *, Lin-wen Hu, On the quenching of steel and zircaloy spheres in water-based nanofluids with alumina, silica and diamond nanoparticles, International Journal of Multiphase Flow 35 (2009) 427–438

2.  Гагаев А.И. Методика и экспериментальная установка для исследования кипения жидкости с добавлением наночастиц в большом объеме

3.  C. Bang, J. H. Joeng Nanotechnology for advanced nuclear thermal-hdraulics and safety: boiling and condensation.