Влияние закрутки потока с помощью ленты, установленной в трубе, на критическую тепловую нагрузку. Кризис теплообмена в закрученных потоках

Лекция 123. Влияние закрутки потока с помощью ленты, установленной  в трубе, на критическую тепловую нагрузкуКризис теплообмена в закрученных потоках

В работах по управляемому термоядерному синтезу, в частности в системах инжекционного нагрева плазмы, плотность тепловых потоков достигает ~100 МВт/м² и реализовать теплосъем в таких условиях возможно с применением закрутки теплоносителя. В ряде работ получено повышение критической тепловой нагрузки до 1,5–2 раз, однако существующие экспериментальные данные и расчетные зависимости для критических тепловых нагрузок противоречивы и расхождение в значениях критической тепловой нагрузки может достигать несколько раз. К тому же отсутствуют массивы согласованных опытных данных для критических тепловых нагрузок при закрутке потока с помощью ленты.

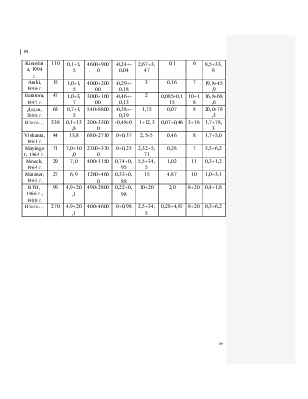
Данные известных работ по критическим тепловым нагрузкам для закрученных с помощью ленты потоков теплоносителя в трубах для отрицательных и положительных паросодержаний обобщены и на основе анализа собранного массива данных получены уравнения.Данные по критическим тепловым нагрузкам при закрутке потока в вертикальных и горизонтальных трубах охватывают следующие диапазоны параметров 0,1<p<20,1 МПа, 0,95<L_H/d<480, 1<y<34,5, 200<rW<39000 кг/м²с, -0,45<x<0,95.

блица 4.2.4.

0,95<L_H/d<480, 1<y<34,5, 200<rW<39000 кг/м²с, -0,45<x<0,95.

При обобщении данных получены уравнения ( 38,391.36, 1.37). Результаты расчета представлены на рис. 1.8784

       (381.36)

где q_кр– расчетная критическая тепловая нагрузка, МВт/м²; ρW – массовая скорость потока, кг/м²с; k_y, k_x, k_l, k – коэффициенты, учитывающие влияние закрутки, недогрева жидкости до температуры насыщения, начального термического участка и давления соответственно

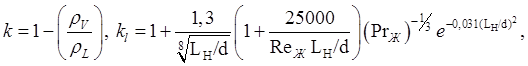
              (1.37)

где x – массовое паросодержание на выходе из трубы; y – коэффициент закрутки потока, равный отношению шага закрутки ленты на 180° к диаметру трубы; r_V и r_L – плотность пара и жидкости на линии насыщения, кг/м³;L_H – длина участка нагрева трубы, мм; d – диаметр трубы, мм; Re_Ж и Pr_Ж – числа Рейнольдса и Прандтля, рассчитанные по температуре жидкости на выходе из трубы. Влияние k_l на q_кр сказывается при L_H/d< 10.

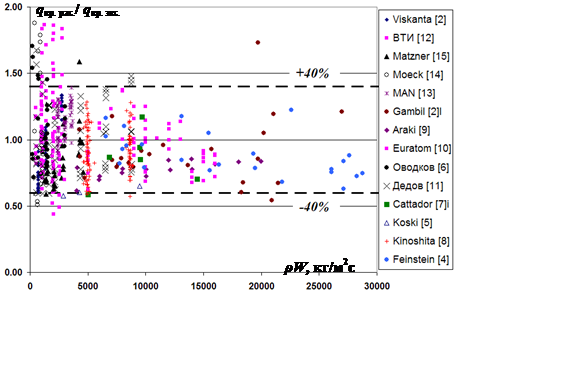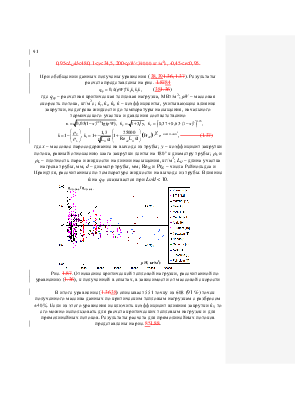
Рис. 1.87. Отношение критической тепловой нагрузки, рассчитанной по уравнению (1.36), к полученной в опытах, в зависимости от массовой скорости

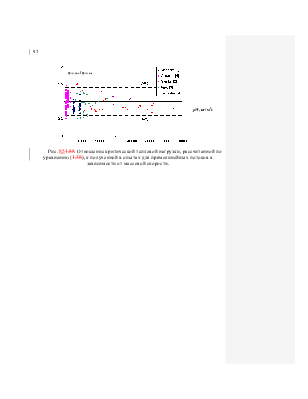
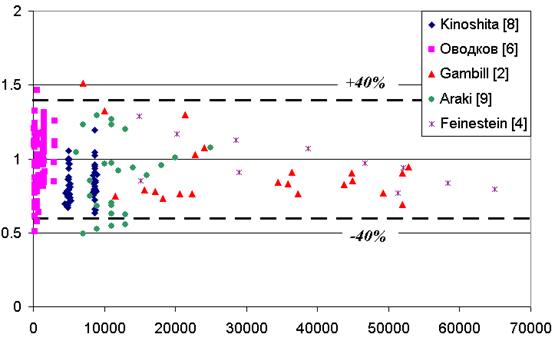
В итоге уравнение (1.3638) описывает 551 точку из 608 (91 %) точек полученного массива данных по критическим тепловым нагрузкам с разбросом ±40%. Если из этого уравнения исключить коэффициент влияния закрутки k_y, то его можно использовать для расчета критических тепловым нагрузок и для прямолинейных потоков. Результаты расчета для прямолинейных потоков представлены на рис.851.88.

Рис. 851.88. Отношение критической тепловой нагрузки, рассчитанной по уравнению (1.38), к полученной в опытах для прямолинейных потоков в зависимости от массовой скорости.