Интенсификация теплоотдачи при течении однофазной среды, страница 3

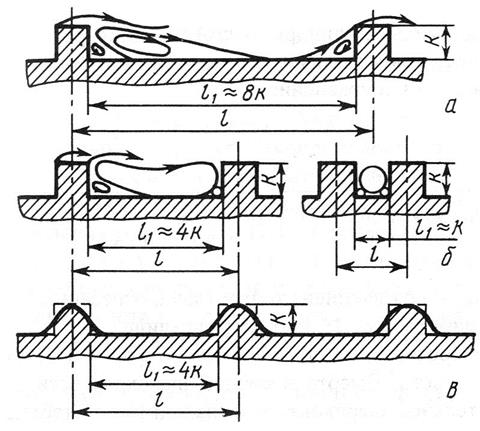
Рис. 2.3. Поверхность с выступами, имеющими прямоугольный (а, б) и плавный (в) профили

При рациональном выполнении искусственной шероховатости можно повысить коэффициент теплоотдачи в два-три раза. Однако важно, чтобы рост теплоотдачи сопровождался не слишком большим увеличением гидравлического сопротивления. Поэтому нерациональны элементы двумерной шероховатости с острыми кромками. Возникающие за ними мощные вихревые зоны и высокое сопротивление формы ведут к большим потерям энергии. Выгоднее элементы шероховатости с плавными очертаниями (см. рис. 2.3 в), для которых характерны меньшие потери энергии. В трубах с плавно очерченными выступами шероховатости при оптимальном отношении l/k увеличение теплоотдачи сопровождается меньшим ростом гидравлического сопротивления, чем в случае шероховатости, имеющей острые кромки.

При достаточно большой относительной шероховатости определенный вклад в увеличение теплоотдачи вносит «эффект оребрения», т.е. увеличение поверхности шероховатой стенки по сравнению с гладкой. Конечно, при условии, что элементы шероховатости имеют хороший тепловой контакт со стенкой. В случае так называемой наложенной шероховатости, например проволоки, расположенной у стенки и не припаянной к ней, эффект «оребрения» отсутствует.

Для расчета теплообмена в шероховатых трубах имеются эмпирические и полуэмпирические зависимости. Полуэмпирические зависимости основываются на двух-, трех- и даже четырехслойных моделях течения вдоль шероховатой стенки. Для каждого слоя подбираются эмпирические зависимости для коэффициентов турбулентного переноса.

Для расчета теплоотдачи в трубах с естественной и искусственной однородной шероховатостью, элементы которой имеют различную форму (проволоки, сферы, пирамиды, цилиндры и др.) и близко расположены друг к другу, так что течение между ними определяется их размерами и формой, Яглом и Кадер предложили уравнение

Здесь Nu=ad / l; a ¾ коэффициент теплоотдачи, отнесенный к поверхности гладкой трубы с диаметром d=2r, взятым во впадине.

Коэффициент сопротивления определяется по формуле Д. Никурадзе для песочной шероховатости. Высота песочной шероховатости, эквивалентная заданной действительной шероховатости, находится по таблице или экспериментально. Уравнение (2.7) справедливо для 100 £ K £ 4000, т.е. для режима с полным проявлением шероховатости при достаточно больших числах Re в диапазонах k/r от 0,005 до 0,18 и чисел Pr от 0,7 до 9. Для указанных условий независимо от формы элементов шероховатости отклонение измеренных чисел Nu от рассчитанных не превышает 10%. Хотя уравнение получено для граничного условия первого рода, им можно пользоваться также при граничном условии второго рода.

“Рациональная интенсификация теплообмена”

“Рациональная интенсификация теплообмена” характеризуется условием

где Nu, x ¾ число Нуссельта и коэффициент гидравлического сопротивления для каналов с турбулизаторами;   ¾ число Нуссельта и коэффициент гидравлического сопротивления для идентичных по геометрии каналов с технически гладкой поверхностью.

Получение опережающего роста теплоотдачи относительно гидравлического сопротивления (2.8) считалось невозможным. Основаниями для этого служили допущения, согласно которым выполняется аналогия Рейнольдса и турбулентное число Прандтля равно единице или по крайней мере постоянно по потоку, и опытные данные для сред с низкими числами Прандтля.

Однако в [2.3, 2.4] показано, что гидродинамическая теория теплообмена не справедлива для турбулентных течений с отрывами, вихревые зоны служат источником дополнительной турбулизации потока и интенсификации теплообмена, и представлены экспериментальные подтверждения соотношения (2.8).