Физика \ Физика

Изучение соударения шаров. Определение коэффициента восстановления относительной скорости, страница 2

Dxокруг. – погрешность округлений.

(15) 

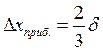
где         Dxприб. – приборная погрешность;

δ – предельная приборная погрешность (равняется 0,25° для круговой шкалы,1мм – для линейки, 1мкс – для счётчика импульсов.

(16) 

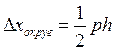
где         Dxокруг. – погрешность округлений;

p = 0,95 – доверительная вероятность;

h – интервал округления (равняется 0,25° для круговой шкалы,1мм – для линейки, 1мкс – для счётчика импульсов.

(17) 

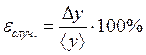
где         εслуч. – относительная погрешность косвенных измерений, с учётом случайной погрешности прямых мзмерений;

Dy – абсолютная погрешность косвенных измерений;

<y> – среднее значение результатов наблюдения.

(18) 

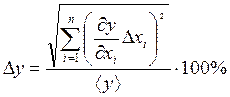
где         Dy – абсолютная погрешность косвенных измерений;

Dxi – абсолютная погрешность прямых измерений;

<y> – среднее значение результатов наблюдения.

(19) 

где         Dxi – абсолютная погрешность прямых измерений;

Dxприб. – приборная погрешность;

Dxокруг. – погрешность округлений;

Dxслуч. – случайная погрешность.

(20) 

где         Dxслуч. – случайная погрешность прямых измерений;

tn,p = 4,30 – коэффициент Стьюдента, при n=3 и p=0,95;

n – количечтво экспериментов;

Dxi – отклонение данного результата от среднего ().

После подстановки соответствующих значений x и y получили следующие формулы для определения относительной погрешности косвенных измерений величин p и F:

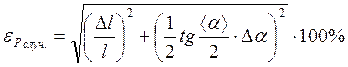
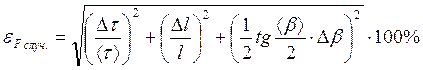
Минимальная погрешность данных косвенных измерений расчитывается также по этим формулам. Отдичие лишь в том, что абсолютные погрешности в формулах включают в себя только приборнуюпогрешность и погрешность округлений, а вместо среднего значения берётся результат первого наблюдения.

Предварительная оценка погрешностей.

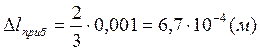
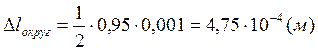
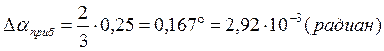
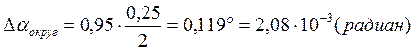
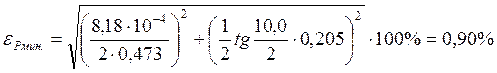
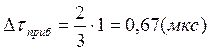
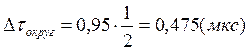
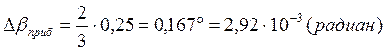
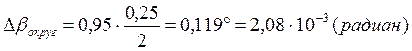
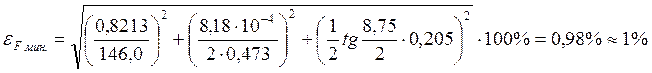
Таблицы с данными, полученными в эксперименте

Расчёт искомых величин.

Опыт1:

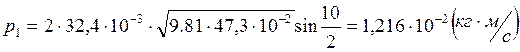
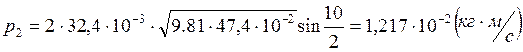
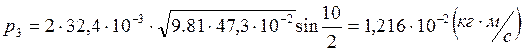
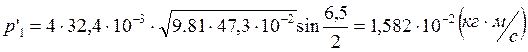
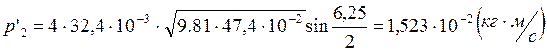
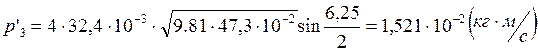
Опыт2:

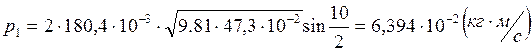
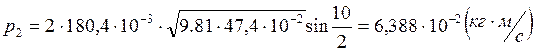
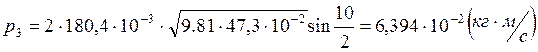
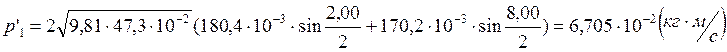
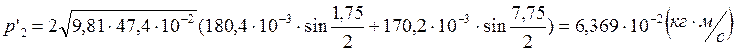
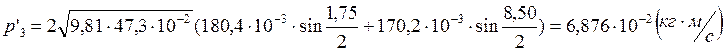
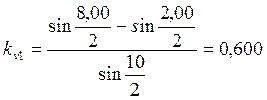
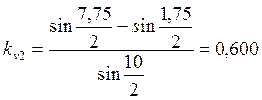
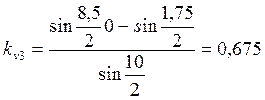
Опыт3:

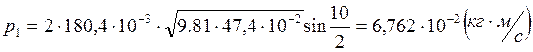
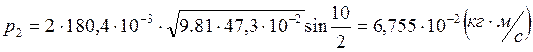
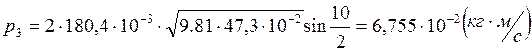
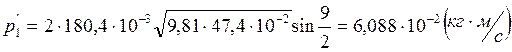
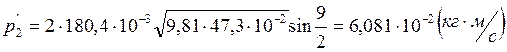
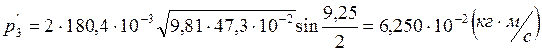
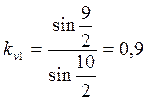
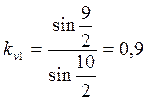
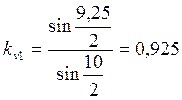
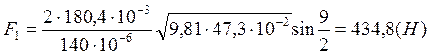
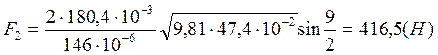
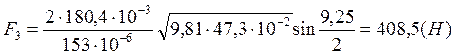
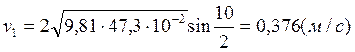
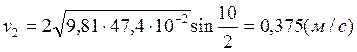
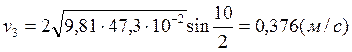
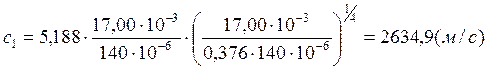
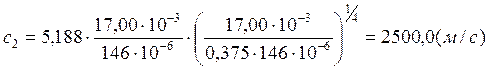
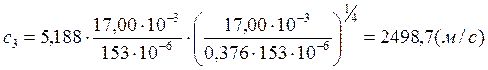
Расчет полных погрешностей.

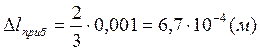
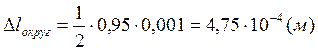
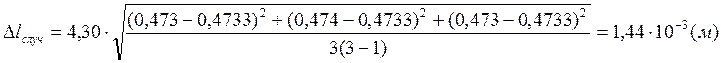
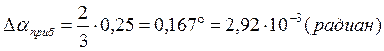
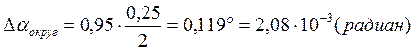
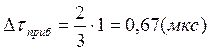
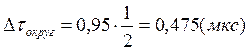
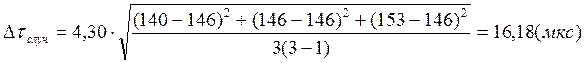
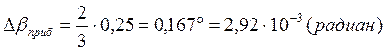
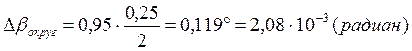
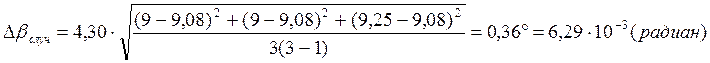
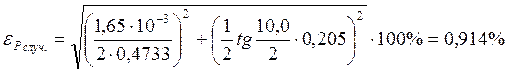
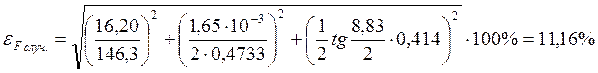
Окончательный результат измерений

,

,


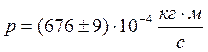Вывод.

В первом опыте рассчитаны импульсы двух пластилиновых шаров до и после столкновения. Столкновение пластилиновых шаров является примером абсолютно неупругого удара. В теории при таком ударе после соприкосновения тел они не восстанавливают полностью свою форму, соединяются вместе и движутся как единое целое с одной скоростью, при этом часть их механической энергии переходит в работу деформации тел (внутреннюю энергию). В результате эксперимента было установлено, что импульс шара до столкновения оказался немного меньше, чем импульс после удара. Это можно объяснить тем, что на практике шары не соединились вместе, а слегка оттолкнулись. Это говорит о том, что это был не абсолютно неупругий удар в чистой форме.

Во втором и третьем опытах также рассчитаны импульсы  до и после столкновения металлических шаров разной массы и металлических шаров одинаковой массы. Столкновения металлических шаров представляет собой абсолютно упругий удар, при котором после взаимодействия тела полностью сохраняют свою форму. Значения импульсов до и после столкновения шаров, полученные в результате эксперимента, оказались близкими по значению, но не равными, что можно объяснить выбором установки для измерения угла отклонения со шкалой с достаточно большой предельной погрешностью , и тем, что такой удар не является абсолютно упругим в полной мере.

Вычислены коэффициенты восстановления относительной скорости. В двух опытах они приближаются к единице, но не равны единице, что свидетельствует, что удар не был абсолютно упругим в полной мере(как известно, для абсолютно упругом удара kv=1,а для абсолютно неупругого kv=0). В случае эксперимента с металлическими шарами одинаковой массы коэффициент ближе к единице, это говорит, что такой удар в большей степени является абсолютно упругим.

Далее рассчитана сила удара двух металлических шаров. Достаточно большую относительную погрешность , можно объяснить выбором установки для измерения угла отклонения со шкалой  с достаточно большой предельной погрешностью (), прибором для измерения времени  соударения (), деревянной линейки для измерения длины подвесы ().

Скачать файл