Вычисление стандартной энтальпии образования газообразных ионов водорода и хлора. Вычисление энергии кристаллической решётки бромида серебра, страница 2

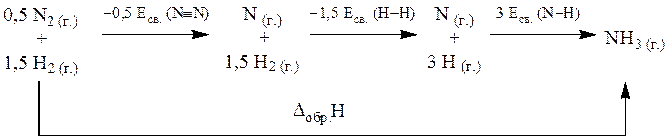
Δ_fH⁰(NH_{3 (г.)}) = 0,5×E_св. (N≡N) + 1,5×E_св. (H–H) + (–3×E_св. (N–H)) =>

E_св. (N–H) = (0,5×E_св. (N≡N) + 1,5×E_св. (H–H) – Δ_fH⁰(NH_{3 (г.)}))/3 = (0,5×940,5 + 1,5×431,46 – (–45,98))/3 = 387,89 кДж/моль.

Ответ: Δ_fH⁰(NH_{3 (г.)}) = 387,89 кДж/моль.

Задача 4. По стандартной энтальпии образования метана (–74,78 кДж/моль), стандартной сублимации графита (714,78 кДж/моль) и энергии связи H–H (431,63 кДж/моль) вычислите среднюю энергию связи C–H.

Решение.

E_св. (C–H) = (Δ_субл.H(C_(гр.)) + 2×E_св. (H–H) – Δ_fH⁰(CH_{4 (г.)}))/4 = (714,78 + 2×431,46 – (–74,78))/3 = 412,21 кДж/моль.

Ответ: Δ_fH⁰(CH_{4 (г.)}) = 412,21 кДж/моль.

Задача 5. Возможно ли протекание следующих  реакций при а) комнатной температуре; б) высоких температурах:

1)  O_{2 (г.)} + 2H₂O _(ж.) = 2H₂O_{2 (ж.)}              ΔH⁰₂₉₈ = 197,28 кДж

2)  2NO _(г.) + O_{2 (г.)} = 2NO_{2 (г.)}                  ΔH⁰₂₉₈ = –601,92 кДж

3)  CaCO_{3 (т.)} = CaO _(т.) + CO_{2 (г.)}             ΔH⁰₂₉₈ = 117,65 кДж

Решение.

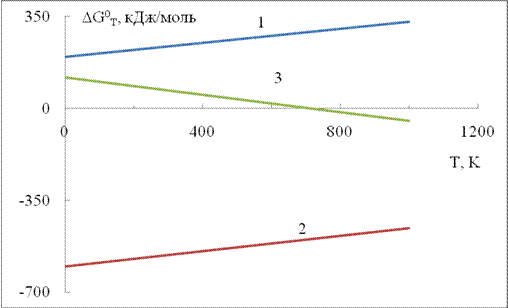
В реакции №1 ΔH⁰₂₉₈ > 0, а ΔS⁰₂₉₈ < 0, так как число моль газов в реакции уменьшается. ΔG⁰_T = ΔH⁰₂₉₈ – T· ΔS⁰₂₉₈ > 0 при любой температуре. Следовательно, эта реакция ни при какой температуре не может идти самопроизвольно. Для неё нельзя подобрать катализатор.

В реакции №2 ΔS⁰₂₉₈ < 0, так как число моль газов в реакции уменьшается. ΔG⁰_T = ΔH⁰₂₉₈ + (–T·ΔS⁰₂₉₈). Первое слагаемое меньше, а второе – больше нуля. Знак ΔG⁰_T определяется знаком того слагаемого, которое больше по модулю. При стандартных условиях ΔG⁰₂₉₈ < 0, так как энтальпия реакции сильно отрицательная величина |ΔH⁰₂₉₈| > |–298·ΔS⁰₂₉₈|. Реакция идёт самопроизвольно, для неё можно подобрать катализатор. При повышении температуры энергия Гиббса реакции становится менее отрицательной величиной, а равновесие смещается в сторону исходных веществ. Если T > (ΔH⁰₂₉₈/ΔS⁰₂₉₈), то ΔG⁰_T > 0. При высоких температурах реакция идёт самопроизвольно в обратном направлении, и никакой катализатор не может сместить равновесие в сторону образования N₂O₃.

В реакции №3 ΔS⁰₂₉₈ > 0, так как число моль газов в реакции увеличивается. ΔG⁰_T = ΔH⁰₂₉₈ + (–T·ΔS⁰₂₉₈). Первое слагаемое больше, а второе – меньше нуля. Знак ΔG⁰_T определяется знаком того слагаемого, которое больше по модулю. При стандартных условиях ΔG⁰₂₉₈ > 0, так как энтальпия реакции сильно положительная величина |ΔH⁰₂₉₈| > |–298·ΔS⁰₂₉₈|. Реакция идёт самопроизвольно в обратном направлении, при стандартных условиях для неё нельзя подобрать катализатор. При повышении температуры энергия Гиббса реакции уменьшается, а равновесие смещается в сторону продуктов. Если T > (ΔH⁰₂₉₈/ΔS⁰₂₉₈), то ΔG⁰_T < 0. При высоких температурах реакция идёт самопроизвольно в прямом направлении, для неё можно подобрать катализатор.

Катализатор не смещает равновесие, так как  он одинаково ускоряет как прямую, так и обратную реакцию. Роль катализатора заключается в более быстром достижении состояния равновесия.

Задача №6. Вычислить приблизительно температуру, при которой константа равновесия реакции CO _(г.) + H₂O _(г.) = CO_{2 (г.)} + H_{2 (г.)} равна единице.

Решение.

Δ_rG⁰_T = –RT·lnK = –RT·lnK = 0.

Подставив полученное значение энергии Гиббса в формулу:

Δ_rG⁰_T = Δ_rH⁰₂₉₈ – T· Δ_rS⁰₂₉₈, получим 0 = Δ_rH⁰₂₉₈ – T·Δ_rS⁰₂₉₈.

Из последней формулы выразим температуру: T = Δ_rH⁰₂₉₈/Δ_rS⁰₂₉₈.

Воспользуемся следствием из закона Гесса, чтобы найти Δ_rH⁰₂₉₈ и Δ_rS⁰₂₉₈.

Δ_rH⁰₂₉₈ = Σn_прод.·Δ_fH⁰_298прод. – Σn_исх.·Δ_fH⁰_298исх. = –393,34 – (–110,44 + (–241,60)) = –41,3 кДж/моль = –41300 Дж/моль.

Δ_rS⁰₂₉₈ = Σn_прод.·S⁰_298прод. – Σn_исх.·S⁰_298исх. = –42,29 Дж/моль.

Найдём температуру.

T = Δ_rH⁰₂₉₈/Δ_rS⁰₂₉₈ = –41300/–42,29 = 977 К.

Ответ: T = 977 К.