Практические занятия по курсу «Химическая термодинамика» (25 задач и их решение)

Практические занятия по курсу

«Химическая термодинамика»

В аудитории студенты решают задачи, подобные представленным ниже.

Домашнее задание: Используя решения, представленные ниже, сформулировать собственные подобные задачи и представить их решения. Каждому студенту необходимо представить не менее одного аналога каждой задачи.  Совпадения предлагаемых вариантов у разных студентов не допустимы. По возможности задачи должны доводиться до численных ответов. Там, где задача решается в общем виде, необходимо использовать другие координаты или предложить более конкретную задачу (перейти к идеальному газу, выбрать конкретное вещество и найти в справочнике необходимые данные и т.д.).

Задача 1

Показать, что бесконечно малое приращение 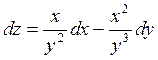  - полный дифференциал.

Это так, если (см. стр. 10, ур. (1.11))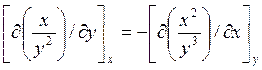   

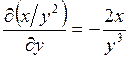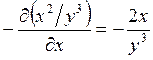 ;      ;  ─ что и требовалось доказать.

Задача 2

Определить теплотворную способность метана (CH).

Теплотворная способность – это количество тепла, выделяющееся при сжигании одного моля вещества. В данном случае необходимо рассмотреть реакцию CH₄+2O₂=CO₂+2H₂O

Теплота реакции на один моль первого вещества   (см. (2.29) на с.16).

Стандартные теплоты образования  кДж/моль,  кДж/моль,  кДж/моль,  т.к. кислород – простое вещество. Следовательно,

 кДж/моль.

Задача 3

Определить необходимое количество воздуха для сжигания 1 л метана (до углекислого газа и воды).

Число молей веществ, участвующих в реакции, пропорционально стехиометрическим коэффициентам уравнения реакции. Т.к., в соответствии с уравнением состояния идеального газа, один моль любого газообразного вещества при заданных температуре и давлении занимает один и тот же объем, то объемы реагирующих веществ также пропорциональны стехиометрическим коэффициентам.

Следовательно, в соответствии  с реакцией горения метана , для одного литра  необходимо 2 литра .Содержание  в воздухе 20%, т.е. воздуха необходимо в 5 раз больше чем кислорода. Требуется 10 литров воздуха.

Задача 4

Определить выделившееся тепло при реакции 1 моля кислорода и 1 моля водорода и состав  продуктов, если теплота образования воды – 241,6 кДж/моль

Уравнение реакции: 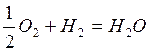. Количество выделившегося тепла (см. (2.24) на с.15) в данном процессе  или . Процесс закончится, как только хотя бы одно из веществ израсходуется. Поэтому координату реакции в момент прекращения горения необходимо находить, как минимальное значение, из соответствующих полному расходованию веществ, участвующих в реакции: 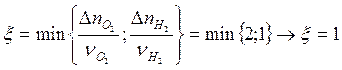 (полностью израсходуется только водород).

Следовательно,  кДж/моль.

Т.к. n_i=n_oi +n_ix (см. (2.22) на с. 15), то состав газа будет таким: O₂ -0.5 моль, H₂ -0 моль, H₂O – 1 моль (учтено, что для реагентов n_i<0, а для продуктов >0).

Задача 5

Определить теплотворную способность этана ().

Теплотворная способность – это количество тепла, выделяющееся при сгорании 1 моля вещества.

В данном случае уравнение реакции 2, ;  

Стандартные теплоты образования  кДж/моль,  кДж/моль,  кДж/моль. Следовательно,

 кДж/моль.

Задача 6

Определить теплотворную способность  природного газа (), если известно, что теплотворная способность метана  кДж/моль, этана кДж/моль.

Теплотворная способность природного газа – это количество тепла, выделяющееся при сгорании одного моля природного газа, следовательно,

, где x_i – мольная доля i-го горючего компонента.

 кДж/моль.

Задача 7

Определить состав продуктов сгорания природного газа , получаемых при его полном сгорании с коэффициентом избытка воздуха 1,2.                  (Состав воздуха ). Определить разность энтальпий исходных реагентов и продуктов сгорания  (в общем виде). Нижние индексы соответствуют температуре.

Пусть сгорает 1 моль природного газа.

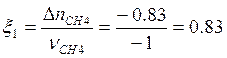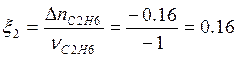;        моль

;  моль

При протекании нескольких реакций изменение числа молей вещества будет равно сумме изменений по каждой j-й реакции, т.е.  . Следовательно,

  моль.

моль.

моль.

Число молей исходного кислорода

моль

Число молей воздуха: 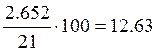моль;

Число молей азота в воздухе:   моль;     

Баланс вещества по каждому компоненту: , откуда  ;          

;

Общее число молей продуктов:

Мольные доли для продуктов

(1) (здесь пр – продукты сгорания, исх – исходная горючая смесь); 

(2) 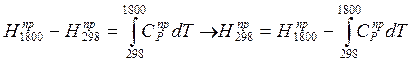(3);

Где DH_298j – теплота j-й реакции при температуре 298К. Складывая (1) и (2), получим

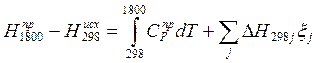
Задача 8

Получить соотношение Максвелла, используя в качестве переменных (p,T).

В этом случае характеристическая функция – энергия Гиббса (см. п. 3.2 и с.24)

; ;

Из первого закона т/д              

, так как G– функция состояния, то       

dG – полный диференциал.

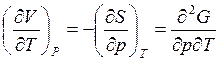
Промежуточный зачет на 6-й неделе

Задача 9

Для стандартных условий (25С) определить, что для идеального газа в координатах T-V наклон изобары      < или > наклона адиабаты.

Наклон кривой в заданной точке определяется производной к этой кривой в данной точке. Т.е. нам необходимо сравнить производные 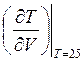для изобарического и адиабатического процесса.

Учтем, что для идеального газа всегда выполняется уравнение состояния PV=RT. Соответственно для 25 ^оС  PV=RT (здесь индекс 25 означает, что все рассматривается при температуре 25 ^оС) 

Изобарa: Из уравнения состояния 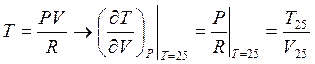  >0

Адиабата: Кроме уравнения состояния для адиабатического процесса выполняется условие . Соответственно,

.

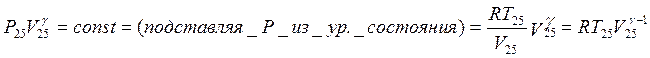
Подставляя далее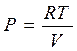

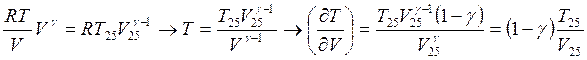
<0, следовательно наклон адиабаты отрицательный

Задача 10

Показать зависимость энтальпии, энтропии и энергии Гиббса для воды в зависимости от температуры T=0-110°C. Вода изменяет фазовое состояние от льда до пара:

H0 – H0298

273

298

373

T, K

                                                              

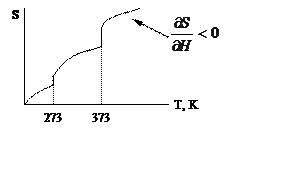à 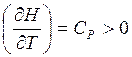 -H – возрастает;   - H –вогнутая крив.

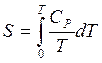à 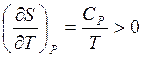 - S – возрастает;  - S – выпуклая крив.           

à   - G -убывает;  - G-выпуклая кривая без скачков, но с разрывом в производной. Скачка нет, т. к. при равновесном фазовом переходе хим. потенциалы фаз (а для чистого вещества хим. Потенциал – это млярная энерг. Гиббса) должны быть равны.

G

  

 

      

 

Задача 11

Используя свойства якобиана (3.38) и (3.36) показать, что

, где

,  .

Действительно,

Задача 12

Показать, что

Указание: использовать выражения для характеристических функций и уравнения Максвелла:

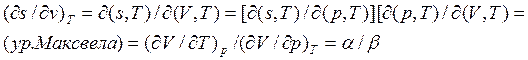
Задача 13

Показать, что .                                                                                                 (1)

В соответствии с (2.7) и (2.14)                                     (2)           

Найдем связь между   и  :                                                                (3)

- дифференциал функции переменных V и T.       (4)

 - см. определение энтальпии (2.8)                                                      (5)

Разделим левые и правые части уравнений (4), (5) на dTпри постоянном pи приравняем правые части

.                   (6)

Откуда, учитывая (2)

,  или

.                                                                                 (7)

Т.к. в соответствии с (3.14) , то

.                                                                                              (8)

Подставляя (8) в (7), получаем

Т.к. из задачи 12   и, учитывая, что по определению ,  и, следовательно ,   то

=

Задача 14

Рассчитать изменение энтальпии и энтропии вещества при переходе без фазовых превращений от Т=1250К и Р=0.1 МПа  к Т=1600К и Р=10 МПа, если известны удельный объём при нормальных условиях (p= 0.1 МПа, T=298K)  = 9,4 см³/моль, коэффициенты термического и объёмного расширения