

3.1 Потоки вызовов, способы задания. Основные характеристики потоков вызовов. Математические модели простейшего и примитивного потоков.
Потоки вызовов – последовательность моментов поступления вызовов в систему обслуживания.
![]()
t1-момент поступления 1-го вызова;
ti-момент поступления i-го вызова;
Способы задания потоков:
Ø Последовательностью моментов времени, когда поступают вызовы.
Ø Последовательностью промежутков между вызовами.
Ø Последовательностью чисел, определяющих количество вызовов в течение отрезка времени:
Классификация : детерминированные и случайные.
Детерминированными - потоки, в которых вызовы поступают в строго фиксированные моменты времени,.
Случайными -потоки, в которых вызовы поступают в случайные моменты времени, я
Рассмотрим потоки, в которых в любой момент времени может поступить не более одного вызова.
Такие потоки могут задаваться:
1. Последовательностью моментов поступления вызовов.
Рис. 1.2 – Первый способ задания потоков вызовов.
2. Поток вызовов задается последовательностью промежутков между вызовами
 |
Рис. 1.3 – Второй способ задания детерминированных потоков.
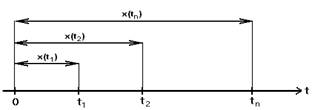 3. Поток вызовов задается последовательностью чисел,
представляющих собой количество вызовов, поступивших в течение отрезка времени.
Введем функцию x(t) – число вызовов, поступивших от начала отсчета до момента
времени t .
3. Поток вызовов задается последовательностью чисел,
представляющих собой количество вызовов, поступивших в течение отрезка времени.
Введем функцию x(t) – число вызовов, поступивших от начала отсчета до момента
времени t .
На практике обычно имеют место не детерминированные потоки, а случайные. В случайных потоках вызовы поступают через случайные промежутки времени и в случайные моменты времени.
Свойства потоков: стационарности, ординарности и последействия.
1. Стационарность потока.
стационарный, если вероятность того, что за время(,t1) поступит x(t0,t1) вызовов.
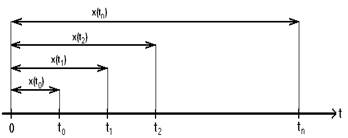 |
Вероятность зависит от промежутков времени и не зависит от временного положения общего начала отсчета – t0 .
вероятность поступления зависит только от отрезка времени [t0,ti); вероятность поступления того или иного числа вызовов зависит от длины временного промежутка и не зависит от его местоположения на оси времени.
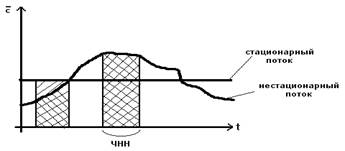 |
Рис. 1.9 – Среднее число вызовов по часам суток.
В ЧНН считают поступающий поток стационарным.
Нестационарным, если вероятность поступления того или иного числа вызовов зависит как от длины отрезка, так и от момента его начала.
2. Последействие потока.
поток с последействием, если вероятность поступления того или иного числа вызовов за некоторый промежуток времени зависит от процесса поступления вызовов до начала рассматриваемого промежутка времени.
потоком без последействия, если вероятность поступления вызова не зависит от процесса поступления вызовов до момента времени t .
3. Ординарность потока.
ординарный, если вероятность поступления 2-х и более вызовов в течение отрезка времени есть бесконечно малая более высокого порядка малости,
Практически ординарность потока означает, что в любой момент времени может поступить не более одного вызова.
Основные характеристики потоков вызовов.
1. Ведущая функция потока вызовов (L);
2. Интенсивность потока вызовов (m);
3. Параметр потока вызовов (l).
Ведущая функция потока L(t1,t2). – среднее число вызовов,поступающих в интервале времени [t1; t2),
Интенсивность потока вызовов m - среднее число вызовов, поступающих в единицу времени.
За единицу времени принимают среднее время обслуживания одного вызова.
Параметр потока l в момент времени t понимается предел отношения вероятности поступления 1-го и более вызовов за отрезок времени [t, t+t] при t ®0 к этому промежутку времени при t® 0
![]()
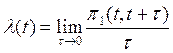
Это плотность вероятности поступления вызовов в момент времени [t,t+t].
Параметр характеризует число вызывающих моментов.
Какова связь между m и l? (теорема Королюка - Зитека)
Для стационарных потоков m.³l
Для стационарных ординарных потоков m=l
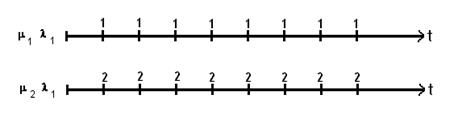
Рис.1.11 - Иллюстрация теоремы Королюка-Зитека .
Пусть на первой оси стационарный ординарный поток с m.1 и l1. В силу выше изложенного m1=l1.
На второй оси показан неординарный поток, т.к. в каждый момент поступает 2 вызова
В каждый момент времени
m2=2m1=2l1
Моменты поступления вызовов зависят от l и определяются им, но l не зависит от того, сколько вызовов поступит в момент времени.
Математических моделей много, на практике используются два потока:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.