Потоки вызовов, способы задания. Основные характеристики потоков вызовов. Нагрузка. Единицы измерения. Способы расчета нагрузки, поступающей в систему обслуживания

единицу времени принимают среднее время обслуживания одного вызова.

 Параметр потока l в момент времени t понимается предел отношения вероятности поступления 1-го и более вызовов за отрезок времени [t, t+t] при t ®0 к этому промежутку времени при t® 0

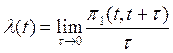
Это плотность вероятности поступления вызовов в момент времени [t,t+t].

Параметр характеризует число вызывающих моментов.

Какова связь между m и l? (теорема Королюка - Зитека)

Для стационарных потоков       m.³l

Для стационарных ординарных потоков             m=l

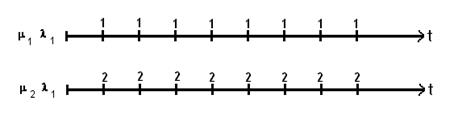
Рис.1.11 - Иллюстрация теоремы Королюка-Зитека .

Пусть на первой оси стационарный ординарный поток с m.₁ и l₁. В силу выше изложенного m₁=l_1.

На второй оси показан неординарный поток, т.к. в каждый момент поступает 2 вызова

В каждый момент времени

m₂=2m₁=2l₁

Моменты поступления вызовов зависят от l и определяются им, но l не зависит от того, сколько вызовов поступит в момент времени.

Математических моделей много, на  практике используются два потока: простейший и примитивный.        

Простейший поток вызовов - это ординарный, стационарный поток без последействия. Такой поток формируется большими группами источников нагрузки. На практике 100 и более абонентов – то поток простейший. (3 способ задания  вызовов)

 

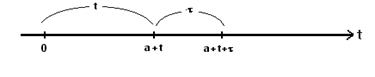В результате получаем формулу Пуассона, которая определяет вероятность того, что на интервале времени (t) поступит точно (k) вызовов.

.  

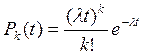Формула Пуассона обладает основным свойством любого закона распределения.

Для стационарных потоков справедливо неравенство m³l. Для стационарных ординарных потоков m=l, т.к. число вызовов совпадает с числом вызывающих моментов.

Симметричным потоком называется поток с простым последействием, параметр которого в любой момент определяется числом обслуживающихся вызовов в этот момент времени и не зависит от других характеристик КС.

Примитивным потоком называется такой симметричный поток, параметр которого - l_i прямо пропорционален числу свободных в данный момент источников:

l_i=(n-i)a , где:     i – число занятых источников;

a - параметр потока одного свободного источника. а примитивного потока – формула Бернулли (t=1):

, где:     n – общее число источников нагрузки, а – удельная нагрузка от одного источника.

3.2 Нагрузка. Единицы измерения. Виды нагрузки. Способы расчета нагрузки, поступающей в систему обслуживания.

Нагрузка - сумма времени занятия всех входов либо всех выходов, либо всех линий пучка за указанный промежуток времени.

Единицей измерения нагрузки часо – занятие (ч. з.).

Интенсивность нагрузки – это математическое ожидание нагрузки за единицу времени.

где:     n – число часов.

Единицей измерения интенсивности нагрузки      

Виды нагрузки:

Поступающая, обслуженная, потерянная.

Обслуженная (У0) – суммарное время занятия пучка линий для обслуживания всех вызовов .

Поступающая нагрузка (У)- это такая обслуженная  нагрузка, когда каждому вызову предоставляется обслуживание в тот час и нет потерь.

Потерянная нагрузка (УП)- называется разность между поступающей и обслуженной нагрузкой за этот промежуток времени.

Уп = У – У₀

Поступающую нагрузку на реальных сетях связи измерить нельзя, т.к. всегда есть потери.

ЧНН (час наибольшей нагрузки) -  непрерывные 60 минут в течение суток, за которые в среднем наблюдается наибольшая интенсивность нагрузки.

Способы расчёта нагрузки:

Упрощённый способ расчёта общей поступающей нагрузки определяется как:  У = ,

Ур – производительная нагрузка (вызовы завершаются разговором).

- параметр;

Рр –доля вызовов, заверш. разговором;

N – число источников нагрузки;

С – среднее число вызовов, поступающих от одного источника в ЧНН;

t_со – среднее время слушанья сигнала станции. Эта величина составляет около 3 с;

t_н/н – время набора одной цифры. Завод диска » 1 с. Возвращение » 0.5 с. Всего » 1.5 с.

t_ус – время установления соединения после набора последней цифры и время разъединения соединения. t_с = 1 с для АТС ДШС. t_с = 2.5 с для АТСК.

t_пв – среднее время посылки вызова в аппарат вызываемого абонента. Эта величина различна в следующих ситуациях: абонент отвечает и абонент не отвечает.

Т – чистое время разговора.

На сети различают следующие категории вызовов:

Ø  общественный сектор N_о;

Ø  квартирный индивидуальный сектор N_ки;

Ø  квартирный коллективный сектор N_кк;

Ø  таксофоны N_т;

Ø  соединительные линии от учрежденческих АТС N _сл;

тогда общее число источников нагрузки равно:

N = N_о + N_ки + N_кк + N_т + N_сл.

3.3 Методы расчета полнодоступных КС в системе с явными потерями (1-я формула Эрланга. Формула Энгсета).

1.  Первая формула Эрланга.

П – простейший поток

S – однозвенная коммутационная система

Сх – полнодоступная (блокировок нет)

Д – явные потери

Приведённая формула Эрланга (все виды потерь равны между собой):

;

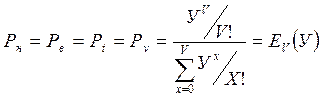Рн – потери по нагрузки;

Рв – потери по вызовам;

Рt – потери по времени;

Рv – вероятность занятости всех обслуживающих приборов (линий);

Еv(У) – вероятность занятости всех приборов при нагрузки У.

Формула табулирована (таблица Пальма)

Область применения: В цифровых ком. полях, т.к. внутренние блокировки малы.

2 Формула Энгсета.

П – примитивный

S – однозвенная коммутационная система

Сх – полнодоступная (блокировки нет)

Все виды потерь не равны.

      ^;       

 ^;

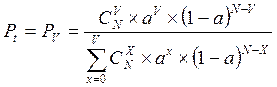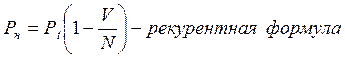
Формула табулирована (таблица Энгсета).

Область применения: в станциях малой емкости с однозвенным полем