
ЭЛЕКТРИЧЕСКИЙ СИГНАЛ И ЕГО ИНФОРМАТИВНОСТЬ.
В основе понимания работы любой электронной аппаратуры лежит теория прохождения электрических сигналов по электрическим цепям. Дадим основные понятия этой теории. Совокупность символов несущих информацию о каком-либо событии или состоянии системы называется сообщением. Сигналом называется физический носитель сообщения. В дальнейшем мы будем рассматривать сигналы, носителем которых является электромагнитное поле. На входе регистрирующей аппаратуры ЭМП создает переменное напряжение, поэтому в дальнейшем под сигналом мы будем понимать именно переменное напряжение (в приборе физическим носителем сигнала становится переменный ток). Параметры сигнала: амплитуда, частота, фаза - для гармонического сигнала; для сложного сигнала - спектр, частота повторения импульсов. Все эти параметры и их изменения несут информацию об объекте исследования.
Сигнал любой формы можно получить путем сложения достаточно большого числа гармоник, т.е. синусоидальных сигналов. Периодический сигнал аналитически можно представить в виде ряда Фурье:
f(t) = Uo + ∑Unsin (nω0t +φn), где U0 - постоянная составляющая сигнала.
Гармоники отличаются амплитудами и фазами, у них кратные частоты.
Спектр сигнала - это набор частот гармоник и соответствующих им амплитуд. Рассмотрим сигналы на рис.
![]()
Спектр сигнала, изображенного на 1 рис., значительно шире, чем у второго, т.е. он содержит значительно больше гармоник.
В некоторых характеристиках сигналов объединяются несколько параметров. Например, форма сигнала зависит от его спектрального состава, т.е. числа гармоник, их амплитуд, фаз.
Для того, чтобы передать информацию с помощью электромагнитных сигналов ее нужно закодировать или, как говорят в радиотехнике, промодулировать сигнал.
Модулирование (кодировка) - совокупность символов и система правил для представления информации с целью ее переработки, передачи, хранения. Способов модулирования несколько, они отличаются степенью защищенности от помех. Рассмотрим некоторые из них (рис.).
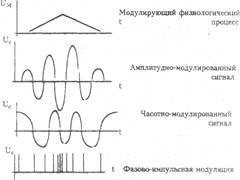
Указанные способы модулирования наблюдаются в диагностических сигналах. Например, фазово-импульсная модуляция используется в ЦНС. Главным информационным элементом центральных кодов мозга является интервал времени между двумя последовательными импульсами.
Различные модуляции различаются между собой степенью защиты от внешних воздействий (помех) и информационной емкостью.
ФИЛЬТРЫ ЭЛЕКТРИЧЕСКИХ СИГНАЛОВ.
Не вся информация может быть актуальна для нас. Возникает вопрос, как выделить существенную, необходимую для диагностики. Эти задачи и решает электронная аппаратура.
Электрические цепи, преобразуя сигналы, изменяют их параметры, что может приводить к потере информации, ее искажению. В основном мы будем рассматривать RC-цепи, понимание процессов в которых достаточно и для понимания общего функционирования электронной аппаратуры. Понимание процессов в RC-цепях полезно еще с одной стороны: физическое моделирование живых тканей, систем, осуществляется, как правило, RC-цепями.
Устройство, пропускающее определенную часть спектра сигнала, называется фильтрам Фильтры широко и разнообразно применяются в медицинской аппаратуре. Одно из применений - борьба с помехами, основной источник которых - электромагнитные поля с частотой 50Гц. В аппаратуре ставятся полосовые фильтры, не пропускающее сигнал с частотой 50Гц, или фильтры, ограничивающие полосу пропускания сигнала от самых низких частот до 50Гц (этой полосы обычно достаточно для медицинской диагностики). Другое применение - машинный анализ медико-биологической информации, например, ЭКГ. Фильтры - основа спектроанализаторов, т.е. устройств, с помощью которых получают спектр сигнала. В них применяют полосовые фильтры, пропускающие определенные частоты. Рассмотрим фильтр низких частот, т.е. устройство, пропускающее низкочастотную часть спектра сигнала (рис.):
![]()
Uвход, Uвых - это входное и выходное напряжения, которые могут меняться по любому закону. Рассмотрим прохождение гармонического сигнала, помня о том, что любой сложный сигнал состоит из гармоник, тогда:
Uвход= Um вх sin(ω t) Uвых = Um вых sin (ωt+ φ0)
Фильтр не изменяет формы синусоидального сигнала. После прохождения фильтра у такого сигнала может измениться (уменьшится) амплитуда и сдвинуться фаза. У сложного сигнала после прохождения фильтра изменяется форма.
Коэффициент
передачи (пропускания) этой цепи равен: ![]()
После
преобразования получим: ![]()
![]()
Полоса пропускания - по уровню К = 1/√2 ≈ 0.7 т.е. от ω = 0 до ωгр = 1/RC.
Можно сказать, что фильтр пропускает те составляющие сигнала, для которых К изменяется от 1 до 0,7. Ясно, что сигнал в некоторой степени искажается и теряет информацию, даже если его спектр попадает в полосу пропускания фильтра. Практика показывает, что это допустимые искажения, т.к. сигналы обычно содержат избыточную информацию.
Рассмотрим фильтр высоких частот (рис.).
![]()
![]()

Обратим внимание, что для К = 1/√2 , снова получим ωгр = 1/RC. Фильтр, пропускающий сигналы в определенной полосе частот, называется полосовым. В качестве примера можно привести следующий фильтр и зависимость К (ω) для него:
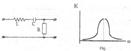
Где ω0 = 1/√LC. На этой частоте индуктивное сопротивление равно емкостному и падение напряжения на участке LC стремится к нулю, поэтому Uвых à Uвх т.е. К à 1.
Напомним,
что импеданс в такой цепи равен ![]()
Если цепочку LC поменять местами с R, то при определенных параметрах можно получить фильтр, подавляющий токи наводок частотой 50 Гц. График для этого фильтра представлен на рис.

Мы видим, что можно получить зависимость К(ω) без аналитического вывода. Для этого нужно сравнить поведение входного и выходного импедансов цепи и распределение напряжений на элементах фильтра при изменении частоты гармонического сигнала.
Например, рассмотрим фильтр с индуктивностью (рис.):
![]()
Zвых не зависит от ω, т.к. Zвых=R. При ω = 0 всё напряжение, приложенное ко входу фильтра, падает на Zвых=R, так как сопротивление индуктивности постоянному току близко к нулю. Следовательно К= 1. При ω à ∞ растет падение напряжения на индуктивности ZL= ωL и тем меньшее напряжение падает на R, т.е. Uвых à 0 и К à 0.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.