Уравнение Бернулли и сопротивление движению жидкости. Определение потерь напора. Местные потери напора

УРАВНЕНИЕ БЕРНУЛЛИ И СОПРОТИВЛЕНИЕ ДВИЖЕНИЮ ЖИДКОСТИ

Уравнение Бернулли для установившегося плавно изменяющегося движения реальной жидкости имеет вид:

где

Гидродинамический напор:

Гидродинамический напор выражает суммарную удельную энергию потока, т.е. энергию, отнесенную к единице веса протекающей жидкости. Потенциальная удельная энергия определяется суммой

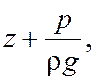
а кинетическая удельная энергия

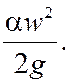
Средняя скорость в сечении определяется из уравнения неразрывности, которое при установившемся движении записывается в виде:

где

В практических расчетах при плавно изменяющемся движении и турбулентном режиме коэффициент Кориолиса принимают равным

При ламинарном режиме вследствие резкой неравномерности распределения скоростей в сечении значение коэффициента Кориолиса значительно больше.

Гидравлический уклон

При изменения потерь напора по линейной зависимости гидравлический уклон равен отношению потери напора к длине, на которой эти потери происходят:

Пьезометрическим уклоном называется уклон пьезометрической линии

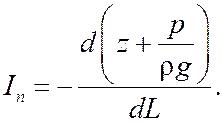
При равномерном движении, когда средняя скорость вдоль потока остается постоянной, гидравлический уклон равен пьезометрическому уклону, т.е.

Режимы движения

При ламинарном режиме движения жидкости частицы жидкости движутся, не перемешиваясь.

При турбулентном режиме движения жидкости частицы жидкости движутся неупорядоченно, хаотически.

Для выяснения режима движения необходимо вычислить число Рейнольдса и сравнить его со значением критического числа Рейнольдса.

Число Рейнольдса, характеризующее режим движения жидкости в напорной трубе:

где

В круглых гладких трубах при Re<2300 режим движения считается ламинарным, а при Re>2300 — турбулентным. При этом из рассмотрения исключается движение жидкости в неустойчивой области. Это приводит к некоторому завышению значений гидравлических сопротивлений в случае, если в этой зоне в действительности имеет место ламинарный режим. Значение числа Рейнольдса Re = 2300 называют критическим.

Для определения режима движения в каналах произвольного сечения в формулу числа Рейнольдса вводят гидравлический радиус, который для кругового сечения равен

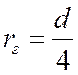
Тогда

Критическое число Рейнольдса при этом принимаем равным 2300.

Значения кинематического коэффициента вязкости пресной воды, м²/с, в зависимости от ее температуры можно приближенно определить по формуле Пуазейля:

Более точные значения кинематического коэффициента вязкости пресной воды приводятся в справочных таблицах.

Определение потерь напора

Общие потери напора условно считают равными сумме потерь напора, вызываемых каждым сопротивлением в отдельности, т.е. применяют так называемый принцип наложения потерь напора.

где

Линейные потери напора вычисляются по формуле:

Где

Для круглой трубы при напорном движении формулу (8) удобно применять в следующем виде:

где

При ламинарном движении коэффициент гидравлического сопротивления является функцией числа Рейнольдса и определяется