Линейные цепи постоянного тока. Определение токов в ветвях, используя первый и второй законы Кирхгофа

Линейные цепи постоянного тока.

1.  Определить токи в ветвях, используя первый и второй законы Кирхгофа. 

2.  В той же цепи  определить токи во всех ветвях методом контурных токов.

3.  Проверить правильность расчетов составлением баланса мощностей.

4.  Начертить потенциальную диаграмму для внешнего контура исходной цепи.

5.  Построить кривую зависимости тока  I₁  от величины сопротивления резистора R₁, используя метод эквивалентного генератора ().

Схема 20   Вариант 20

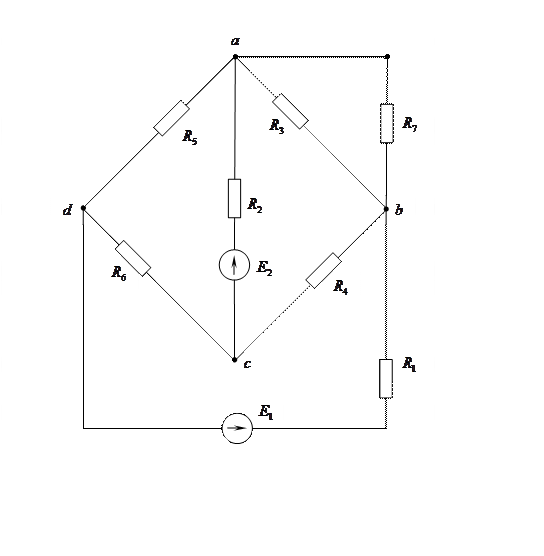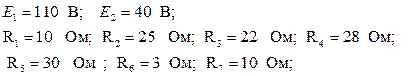
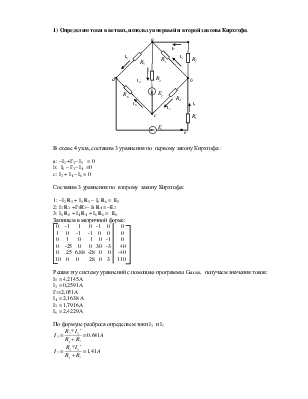
1) Определим токи в ветвях, используя первый и второй законы Кирхгофа.

 

В схеме 4 узла, составим 3 уравнения по  первому закону Кирхгофа :

a: –I₂ +I'₃– I₅   = 0

b:  I₁ – I'₃– I₄  =0 

c: I₂ + I₄ – I₆ = 0

Cоставим 3 уравнения по  второму  закону Кирхгофа:

1: –I₂ R₂ + I₅ R₅ – I₆ R₆ =  E₂

2: I₂ R₂ +I'₃R'₃– I₄ R₄ = –E₂

3: I₁ R₁ + I₄ R₄ + I₆ R₆ =  E₁

Запишем в матричной форме:

  0    -1      1      0   -1    0        0

1     0     -1     -1    0    0        0

0     1      0       1    0   -1       0

0    -25    0      0   30   -3      40

0     25  6.88  -28   0    0     -40

 10    0     0       28   0    3     110

 

Решая эту систему уравнений с помощью программы  Gauss,  получаем значения токов:

I₁ = 4,2145A

I₂ = 0,2591A

I'₃=2,051A

I₄ = 2,1638 A

I₅ = 1,7916A

I₆ = 2,4229A

По формуле разброса определяем токи I₃  и I₇

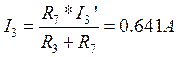
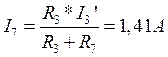
2) Определим все токи методом контурных токов:

R₁₁ I₁₁ + R₁₂ I₂₂ + R₁₃ I₃₃ = E₁₁

R₂₁ I₁₁ + R₂₂ I₂₂ + R₂₃ I₃₃ = E₂₂

R₃₁ I₁₁ + R₃₂ I₂₂ + R₃₃ I₃₃ = E₃₃

(R₂ + R₅ + R₆) I₁₁ – R₂ I₂₂ – R₆ I₃₃ =   E₂

– R₂ I₁₁ + (R₂ + R'₃ + R₄) I₂₂ – R₄ I₃₃ =– E₂

– R₆ I₁₁ – R₄ I₂₂ + (R₁ + R₄ +R₆) I₃₃ =  E₁

58 I₁₁ – 25 I₂₂ - 3 I₃₃ = - 40

- 25 I₁₁ + 59.88 I₂₂ - 28 I₃₃ = 40

- 3 I₁₁ – 28 I₂₂ + 41 I₃₃ = -110

Решая это уравнение с помощью программы  Gauss,  получаем значения контурных токов:

I₁₁ = 1,7917А        

I₂₂ = 2,051А       

I₃₃ = 4,2147А

I₁ = I₃₃ = 4,2147A

I₂ = I₂₂ – I₁₁  = 0,2593A

I'₃= I₂₂=  2,051A

I₄ = I₃₃– I₂₂  = 2.1637 A

I₅ = I₁₁ = 1.7917A

I₆ = I₃₃– I₁₁  =  2.423A

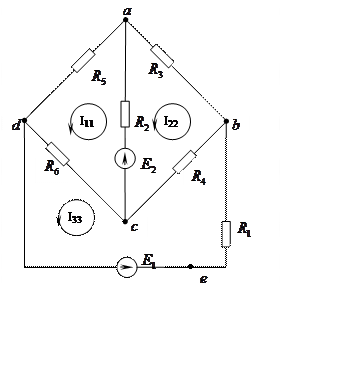
По формуле разброса определяем токи I₃  и I₇

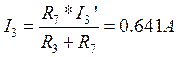
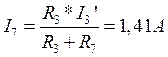
3) Составим баланс мощностей:

ΣP_ист = E₁ I₁ – E₂ I₂  = 453,2  Вт

ΣP_пр = R₁ I₁² + R₂ I₂² + R₃ I₃² + R₄ I₄² + R₅ I₅² + R₆ I₆² + R₇ I₇²  = 453,8 Вт

ΣPист ≈  ΣPпр

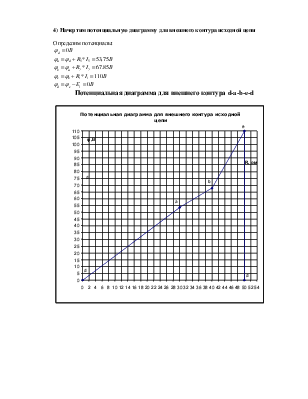
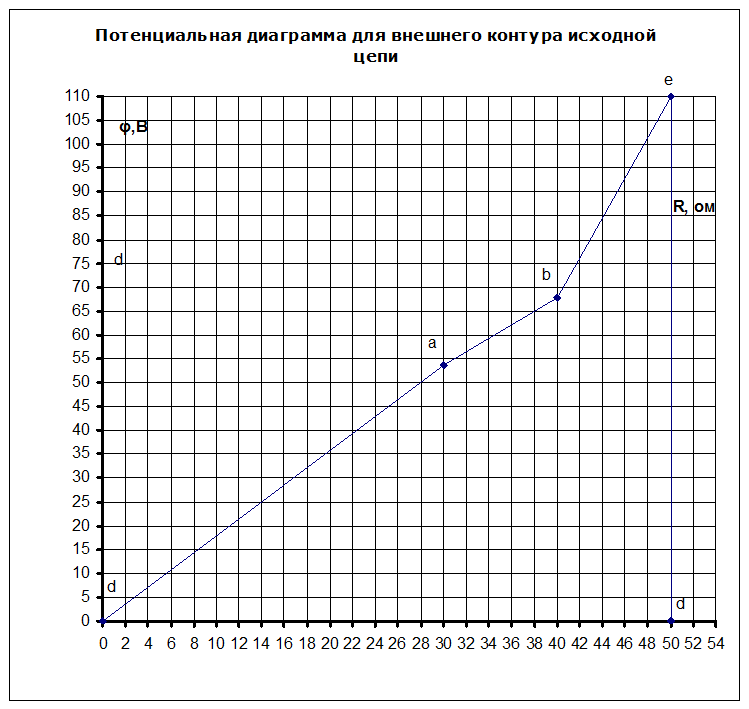
4) Начертим потенциальную диаграмму для внешнего контура исходной цепи

Определим потенциалы:

Потенциальная диаграмма для внешнего контура d-a-b-e-d

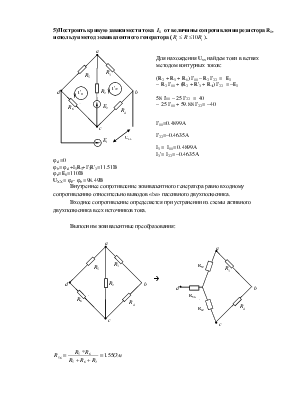
5)Построить кривую зависимости тока  I₁  от величины сопротивления резистора R₁, используя метод эквивалентного генератора ().

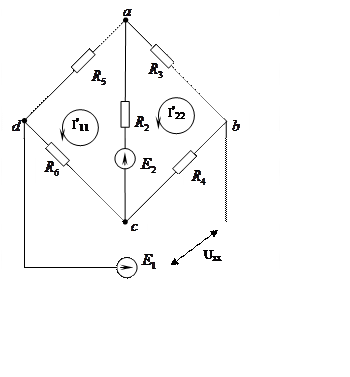
Для нахождения U_xx найдем токи в ветвях методом контурных токов:

(R₂ + R₅ + R₆) I'₁₁ – R₂ I'₂₂ =   E₂

– R₂ I'₁₁ + (R₂ + R'₃ + R₄) I'₂₂  = –E₂

 

58 I'₁₁ – 25 I'₂₂  =  40

– 25 I'₁₁ + 59.88 I'₂₂ = –40

I'₁₁=0.4899A

I'₂₂=–0.4635A

I₅ =  I₁₁= 0.4899A

I₃'= I₂₂= –0.4635А

φ_d =0

φ_b= φ_d +I₅R₅+I'₃R'₃=11.51В

φ_e=E₁=110В

U_XX= φ_e– φ_b =98.49В

Внутреннее сопротивление эквивалентного генератора равно входному сопротивлению относительно выводов «be» пассивного двухполюсника.

Входное сопротивление определяется при устранении из схемы активного двухполюсника всех источников тока.

Выполним эквивалентные преобразования:

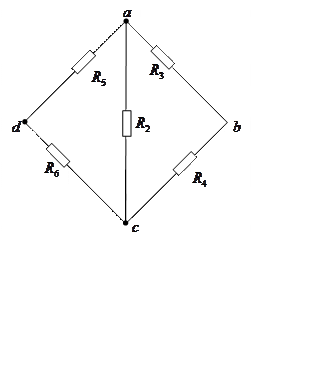
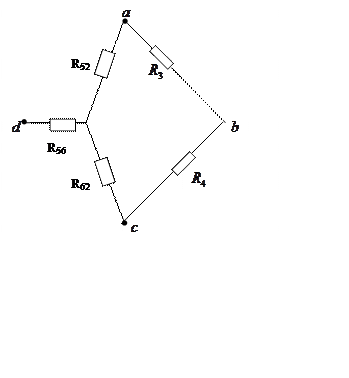
è

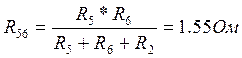
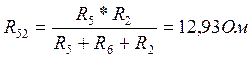
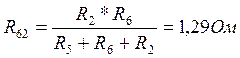
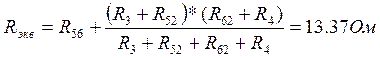
Тогда,  I₁=U_XX/( R_экв+R₁)= 4,2147A

Результат сошелся с результатами, полученными в п. 1,2,3

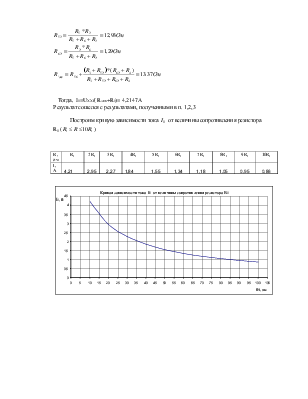
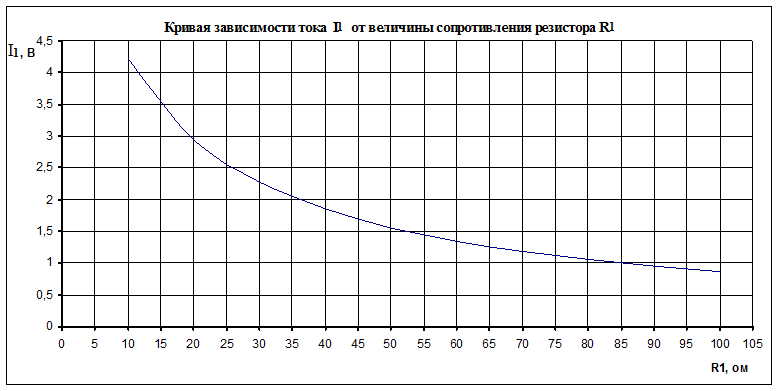
Построим кривую зависимости тока  I₁  от величины сопротивления резистора R₁ ()

R, ом	R1	2R1	3R1	4R1	5R1	6R1	7R1	8R1	9R1	10R1
I, A	4,21	2,95	2,27	1,84	1,55	1,34	1,18	1,05	0,95	0,86