



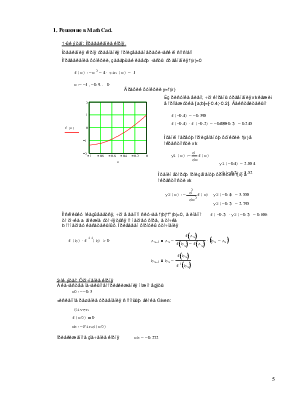








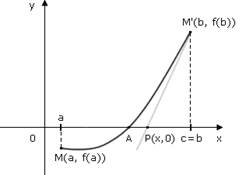
Идея способа хорд состоит в том, что можно с известным приближением допустить, что функция на достаточно малом участке [а, b] изменяется линейно. Тогда кривую у = f(х) на участке [а, b] можно заменить хордой и в качестве приближенного значения корня принять точку пересечения хорды с осью абсцисс. Для лучшего выяснения сути способа обратимся к чертежу (рис.):
Построим график функции у = f(х) на участке [а, b]. Истинный корень уравнения f(x) = 0 есть абсцисса точки А, являющейся точкой пересечения кривой ММ' с осью абсцисс.
Заменив кривую ММ' хордой ММ', мы примем в качестве приближенного значения корня абсциссу точки В, в которой хорда пересекается с осью.
Напишем уравнение прямой,
проходящей через точки M(a, f(a)) и M'(b, f(b)): ![]()
Абсцисса точки В, являющаяся приближенным корнем x1 уравнения f(x) = 0, может быть найдена из уравнения прямой, если положить в нем у = 0. Тогда получим
![]() или, иначе:
или, иначе: ![]()
Уравнение рассматриваемой прямой можно записать и в таком виде:
![]() Полагая здесь у = 0, придем к формуле
Полагая здесь у = 0, придем к формуле ![]()
Очевидно, формулы (*) и (**) тождественны. Мы будем пользоваться той из них, которая окажется более удобной.
Полученное значение x1 можно снова использовать для дальнейшего уточнения корня по способу хорд, рассматривая интервал [а, x1] или же [x1, b], смотря по тому, в каком из них лежит истинный корень. Чтобы определить это, находят знак f(x1).
 Метод касательных (способ
Ньютона)
Метод касательных (способ
Ньютона)
Рассмотрим
уравнение f(x) = 0. Возьмем
некоторую точку с участка c ![]() [a, b] и проведем в точке [c, f(c)] графика функции касательную к
этому графику (рис.). Уравнение касательной имеет вид: y-f(c) = f’(c)(x-c).
[a, b] и проведем в точке [c, f(c)] графика функции касательную к
этому графику (рис.). Уравнение касательной имеет вид: y-f(c) = f’(c)(x-c).
В качестве приближенного корня
уравнения примем абсциссу точки пересечения касательной с осью Ох. Полагая в
уравнении касательной y = 0, находим для абсциссы точки
пересечения:![]()
Остается решить вопрос о выборе точки с.
На рисунке мы выбрали c = b. Обычно принимают c = a или c = b, смотря по тому в какой из этих точек знак функции совпадает со знаком второй производной, т. е. с выбирают так, чтобы произведение f(c)*f’’(c) > 0.
В этом случае можно гарантировать, что приближенное значение корня x2, полученное по способу касательных, лежит на интервале [a, b].
Как и в способе хорд, значение x2 можно использовать для дальнейшего уточнения корня, беря интервал [a, x2] или [x2, b].
Комбинированный способ
Рассмотренные примеры показывают, что способ хорд и способ касательных дают приближение корня с разных сторон (больше или меньше истинного корня). Такой характер приближения имеет место всегда. Поэтому обычно бывает выгодно применять оба эти способа одновременно, благодаря чему уточнение корня может быть получено быстрее.
Ограничения, наложенные на функцию и отрезок интервала изоляции, дают нам только 4 возможных случая, в которых точка х*, изображающая точный корень уравнения расположена между приближенным корнем х1, полученным по методу хорд, и приближенным корнем х2, полученным по методу касательных.
Задание:
Решить уравнение ![]() с предельной абсолютной погрешностью
ε=0.0001 (при решении в Excel ε=0.005)
с предельной абсолютной погрешностью
ε=0.0001 (при решении в Excel ε=0.005)
Решение:
Осуществляется с помощью математического пакета MathCad, электронных таблиц Excel и транслятора языка BASIC – Microsoft Visual Basic.
1. Решение в MathCad.
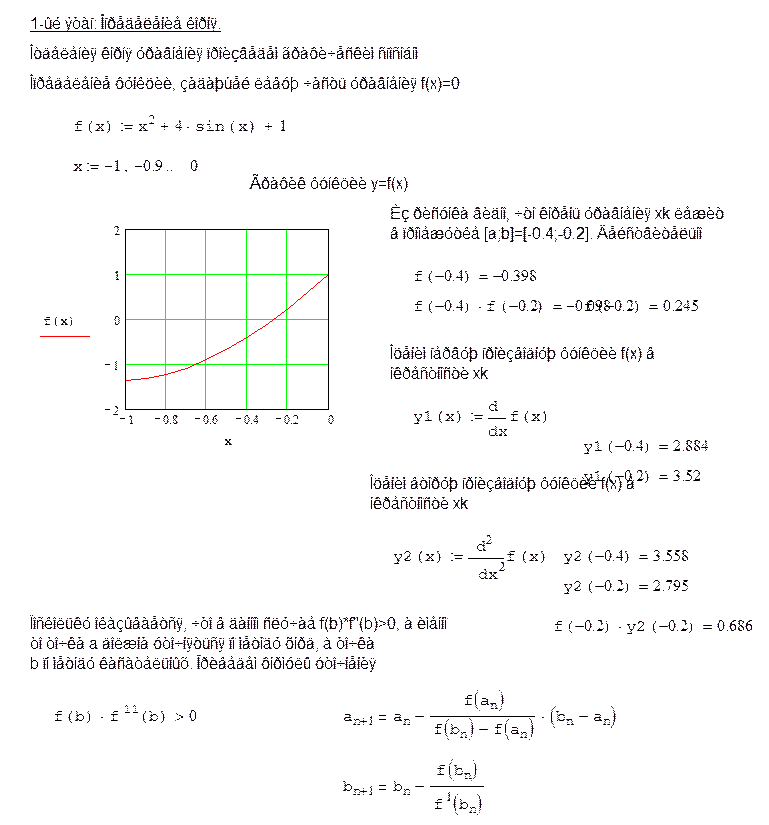
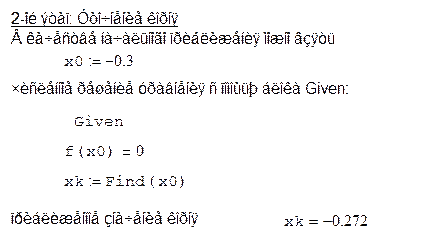
2. Решение в Excel.
|
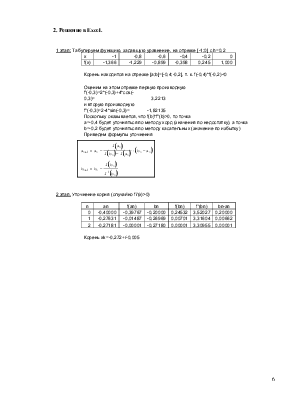
1 этап: Табулируем функцию, задавшую уравнение, на отрезке [-1;0] с h=0,2 |
|||||||||
|
x |
-1 |
-0,8 |
-0,6 |
-0,4 |
-0,2 |
0 |
|||
|
f(x) |
-1,366 |
-1,229 |
-0,899 |
-0,398 |
0,245 |
1,000 |
|||
|
Корень находится на отрезке [a;b]=[-0,4;-0,2], т. к. f(-0,4)*f(-0,2)<0 |
|||||||||
|
Оценим на этом отрезке первую производную |
|||||||||
|
f'(-0,3)=2*(-0,3)+4*cos(-0,3)= |
3,2213 |
||||||||
|
и вторую производную |
|||||||||
|
f"(-0,3)=2-4*sin(-0,3)= |
-1,82135 |
||||||||
|
Поскольку оказывается, что f(b)*f"(b)>0, то точка |
|||||||||
|
a=-0,4 будет уточняться по методу хорд (значения по недостатку), а точка |
|||||||||
|
b=-0,2 будет уточняться по методу касательных (значение по избытку) |
|||||||||
|
Приведем формулы уточнения |
|||||||||
|
|
|||||||||
|
2 этап. Уточнение корня (случайно fi'(x)>0) |
|||||||||
|
n |
an |
f(an) |
bn |
f(bn) |
f'(bn) |
bn-an |
|||
|
0 |
-0,40000 |
-0,39767 |
-0,20000 |
0,24532 |
3,52027 |
0,20000 |
|||
|
1 |
-0,27631 |
-0,01487 |
-0,26969 |
0,00701 |
3,31604 |
0,00662 |
|||
|
2 |
-0,27181 |
-0,00001 |
-0,27180 |
0,00001 |
3,30955 |
0,00001 |
|||
|
Корень xk=-0,272+/-0,005 |
|||||||||
3. Решение в BASIC.
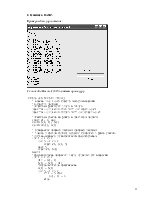
Примерный вид приложения:
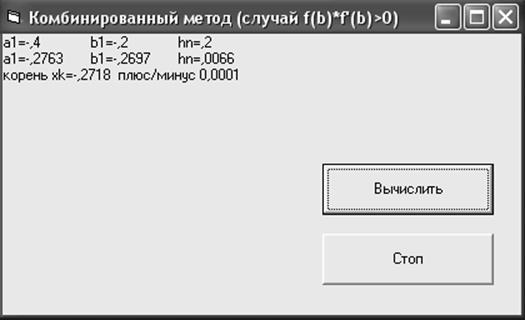
Перейдя в окно кодов, в области General опишем функцию, задающую уравнение:
Private Function f(x)
' описание функции, задающей уравниние
f = x * x + 4 * Sin(x) + 1
End Function
Private Function f1(x)
' описание функции, задающей первую производную от f(x)
f1 = 2 * x + 4 * Cos(x)
End Function
С кнопкой «Вычислить» свяжем процедуру
Private Sub btnCalc_Click()
' уточнение корня комбинированным методом
' *********************************
' f(x)=0 *
' *********************************
' случай
' *********************************
' f(b)*f''(b) > 0 *
' *********************************
' [a,b]- отрезок содержащий корень уравнения
' a1, a2-два последовательных приближения корня по недостатку
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.