Дискретные системы управления. Передаточные функции (матрицы) замкнутых систем. Устойчивость дискретных систем. Синтез регуляторов для дискретных объектов с полной информацией

Свойства замкнутых систем с динамическим регулятором с устройством оценки пониженной размерности

Постановка задачи:

Задан объект управления с неполной информацией c уравнением движения:

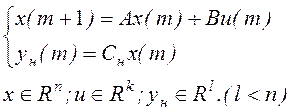
пара А,В – полностью управляема;

пара ,А- полностью наблюдаема;

rank=l

Будем строить динамический регулятор с устройством оценки пониженной размерности по следующим уравнениям движения:

с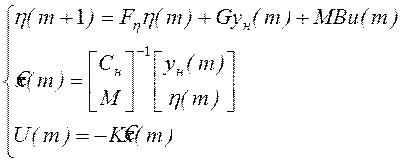  

 - вектор состояния устройства оценки

 - вектор оценки

 - опред. свойства

 - матрица входов устройства оценки

 - матрица ЛСОС

Задача синтеза динамического регулятора с устройством оценки пониженной размерности заключается в выборе таких матриц описания устройства оценки  и  , а также матрицы преобразования М и матрицы ЛСОС К, которые обеспечивают замкнутой системе желаемые динамические свойства.

Рассмотрим свойства замкнутой системы:

Запишем уравнение движения замкнутой системы, объединив уравнения движения объекта и динамического регулятора.  Замкнутая система :   

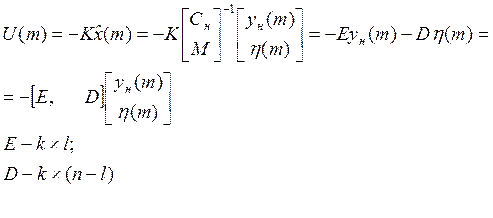
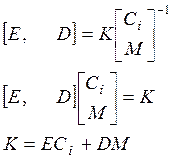
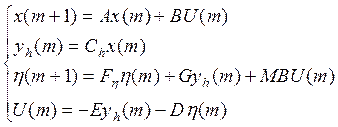Вычтем из уравнения движения устройства оценки уравнение движения объекта, слева умноженное на матрицу преобразования М, тогда:

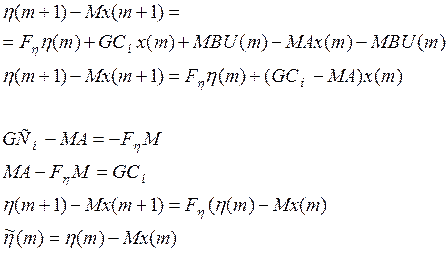
   -вектор невязки,  тогда

Замкнутая система: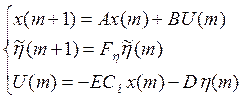

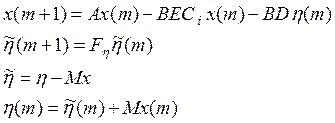
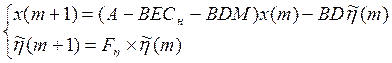
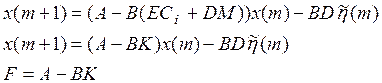
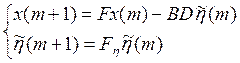
Перепишем уравнение движения системы в блочно-матричной форме:

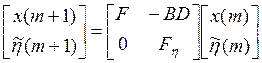
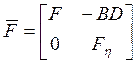  - (2n-l) (2n-l) – матрица описания замкнутой системы

Из верхнетреугольного вида блочной матрицы описания замкнутой системы следует что характеристическое уравнение замкнутой системы – есть произведение характеристических матриц  и  , а корни замкнутой системы есть объединение корней характеристических полиномов матриц  и  , т.е. :

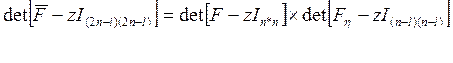
2n-l                           n                           n-l

Если обозначить  - корни характеристического полинома матрицы F, а  - корни характеристического полинома матрицы

 

2n-l

Свойство разделения:

1)  n желаемых корней замкнутой системы можно обеспечить выбором матрицы ЛСОС, т.е. для матрицы F=A-BK

2)  Оставшиеся n-l корней можно обеспечить назначением матрицы описания устройства оценки .

Процедура синтеза динамического регулятора с устройством оценки пониженной размерности с использованием метода модального управления.

Динамический регулятор: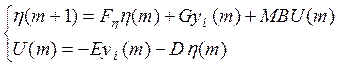     

, G - ? ;   M, К - ? ;   K(E,D) - ?

Определение матрицы ЛСОС К

А, В – полностью управляемы - ?

По требованию динамическим свойствам замкнутой системы назначение n желаемых корней замкнутой системы или коэффициентов характеристического полинома

По желаемым корням или коэффициентам характеристического полинома формирование матриц эталонной модели Г в одном из канонических видов и выбор матрицы выходов эталонной модели Н из условия полной наблюдаемости пары Н,Г

Решение матричного уравнения типа Сильвестра, относительно матрицы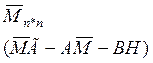

С последующим вычислением ЛСОС

Формирование матриц описания устройства

1. Проверка ,А на полную наблюдаемость, rank=1

2. Исходя из требуемой скорости сходимости           вектора оценки к оцениваемому вектору назначение оставшихся n-l желаемых корней характеристического полинома (или коэффициентов)

3. По желаемым корням или коэффициентам характеристического полинома формирование матрицы описания устройства оценки -(n-l)  (n-l) в одном из канонических видов и выбор матрицы входов устройства оценки G – (n-l) l из условия полной управляемости пары  

4. Решение уравнения типа Сильвестра относительно матрицы преобразования M-(n-l) n

5.Нахождение произведения МВ и вычисление матриц E,D по соотношению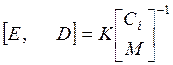

Пример:

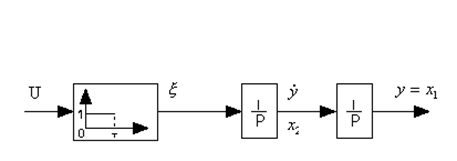
Требуется построить динамический регулятор  с устройством оценки пониженной размерности, обеспечивающее в замкнутой системе оптимальность по быстродействию.

Предположим: измеряется только устройство.

Пусть:

Т=1с

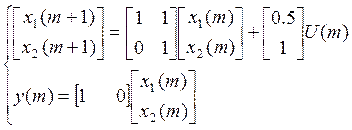
Будем строить динамический регулятор в соответствии с уравнениями