Amergansy forcasting in DC-DC buck converter dynamics, страница 2

The algorithms of PECS dynamics identification and forecasting are realized with the help of the programmable logical array (PLA). Advantages of it usage are the following: large capacity; availability of software; capability of multiple reprogramming; simplicity of existent software usage; capability of parallel data processing by each canal; and high speed processing that is one of the most important from the point of the real-time operation mode realization view. If the data processing subsystem forecasts an emergency possibility, this subsystem forms the necessary control action that allows DC–DC buck converter to continue working in the operation mode that has been planned in advance. It is realized hardwarily due to the cooperation between the data acquisition and the control subsystems that allows changing the transfer constant of the proportional unit automatically.

Slow data processing is aimed at data acquisition for their future analysis and preliminary information forming about DC–DC buck converter dynamics. For this purpose the power stage output voltage and throttle current through corresponding sensors and width-pulse modulator output voltage come to ADC board from the data acquisition subsystem. These three signals are transformed into 12-digit code, saved to Hard Disk of IBM-PC that allows time series researching and time series processing in according to algorithms of data base forming.

It is necessary to please height emphasis on the timeless diagnostics of stability loss, conformably to the problem of emergency forecasting in DC-DC buck converter dynamics. In particular, we talk, first of all, about the scenario of dynamics evolution in the chaos direction by means of period doubling 1-2-4. This scenario is one of the most widespread in PECS dynamics, that was shown through investigations on the experimental plant [4]. At that the first bifurcation forecasting is very important because divisible reduction of frequency of energy conversion process and incising amplitude characteristics of signals are the results of each bifurcation in the context of this scenario. 

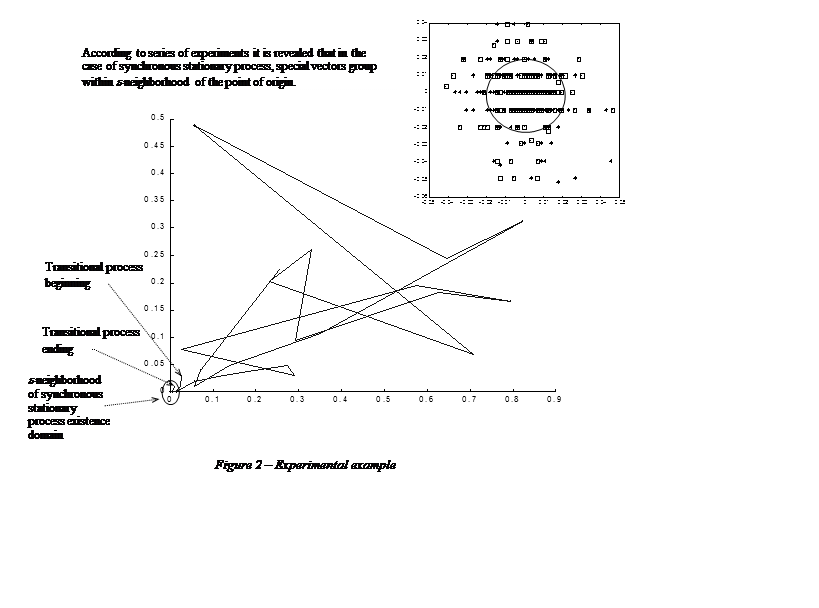
Correspondingly, first of all, the efficiency researches of the fractal approach [3] were carried out just from this point of view. Fractal regularities are considered from the geometrical point of view. They are expressed in that, that a set of phase trajectories of one type stationary process, generated through the consecutive parameter variation, represents similar geometrical structures with certain shape (size and rotation) modifications. It allows presenting the stationary process geometrical image in a specialized 2-D stereo-projection by means of one fixed vector and structurizing of a set of the fixed vectors in the form of each type stationary process existence domains (for example synchronous process existence domain represents a point of origin Fig. 2).

At the same time, the transitional process geometrical image is presented by means of a trajectory in the specialized 2-D stereo-projection. A direction of the trajectory indicates the domain of a stationary process, setting of which is forecasted. It is essential to note that experimental time series include “noise” that is stipulated by different disturbances. It is expressed in a fuzzy character of boundaries of stationary process existence domains that is illustrated in the figure 2 a. At the example (Fig. 2 b.) is shown that the present transient trajectory “terns” into neighborhood of a point of origin in the result of this process completing. It allows making a decision about convergence to a stationary process and an emergency will not realize.                      

Conclusion:

A comparative analysis of numeric and experimental results shows their satisfactory conformity in general. So, there is a fundamental possibility to use the approach [3] to real-time emergency forecasting in DC-DC buck converter dynamics. Though, the further experimental researches are necessary that will be directed at consideration f possible variants of dynamic evolution in DC-DC buck converter, functioning under any noise disturbances. 

References

[1] A.L. Aroudi and R. Leyva, “Quasi-periodic route to chaos in a PWM voltage-controlled dc-dc boost converter”, IEEE Trans.on Circuits and Systems, vol.48, No 8, 2001, pp. 967-978.

[2] H.H.C. Iu and C.K. Tse, “Bifurcation behavior in parallel-connected buck converters”, IEEE Trans. on Circuits and Systems, vol 48, No. 2, 2001, pp. 233-240.

[3] Yu. Kolokolov and A.Monovskaya, “Fractal principles of multidimensional data structurization for real-time pulse system dynamics forecasting and identification”, Chaos, Solutions & Fractals, vol.25, No. 5, 2005, pp.991-1006.

[4] Yu.V.Kolokolov, S.L. Koschinsky and V.V. Bagrov, “Experimental dynamics of electromechanical pulse energy conversion systems”, Proc. of the IEEE 2^nd Workshop “On Intelligent Data Acquisition and Advanced Computer Systems: Technology and Applications (IDAACS’2003)”, Lviv, Ukraine 8-10 Sept., 2005, pp.300-304.