Forming special observer structures, страница 2

The analysis of the equations (10)-(12) confirms, that the observer structure (choice of matrix ) influences on estimate errors. In each concrete case (for concrete object), errors may be numerically analyzed and formed in determine limits.

In the system with the observer, modal regulator can be divided into two sub objects:

                                             (13)

first part  «works» with measurable state-variables, second  - with immeasurable state-variables. Let’s write equations (5), (6), (10) and (11) in operate form and taking into consideration (13), the equation for closed-loop system may be written:

           (14)

from equation (14) it can be seen, that the system reaction on the external uncontrolled influence depends on observer structure (matrix ). And there is an opportunity to choose special observer structure for forming systems with different extant invariantion on external uncontrolled influence (especially in static regime).

Example

In accordance with equations (1), (2) controlled and observed 4-order object () with a single input () and single output (), with two measurable state-variables () is given a:

  

   

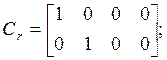
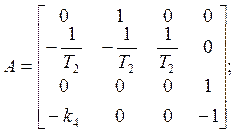
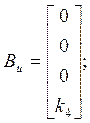
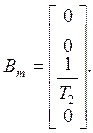
According to Luenberger’s method of projecting reduce-order observers [3] the object can be divided into two sub objects (7), (8), where

 

         

            

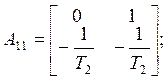
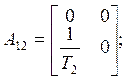
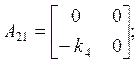
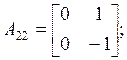
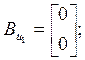
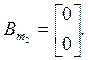
Using (5), (6) regulator equation may be written as:

where

After putting the observer into the system a matrix of coefficients according to (13) can be separated on two parts    

Supposing that all state-variables can be measured, there are no problems to calculate modal regulator coefficients, for example with a standard binomial form:

.

To reduce elementary transforming the final result is given:

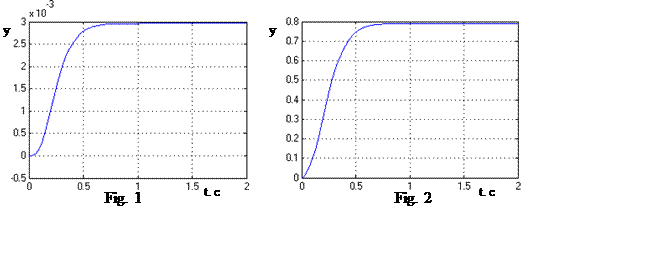
when . In Fig. 1, 2 graphics of transfer characteristics of system on input (Fig. 1) and external uncontrolled (Fig. 2) influences are introduced.

From Fig. 2 one can see that the system reaction on external uncontrolled influences isn’t satisfied.

Projecting of observer for estimating immeasurable state-variables  is realized below. In accordance with (9) observer matrix of coefficients for this object may be written:

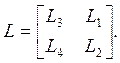
The observer is 2–ordered, its dynamics set up on Butterworth’s standard form:

The coefficients near the same degrees are leveled, as a result two equations with four unknown coefficients of matrix  are got. So it is possible to choose two coefficients arbitrary (they can be also equal zero), and form different structures.

Let  Determine from (12) static errors vector:

so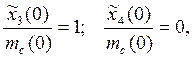

this means, that trough  of modal regulator in spite of real state-variable signal , equal  will enter.

To understand, how this observer structure influences the system, it is necessary to analyze the equation (14) for static regime. As a result 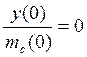. For given the reason the system becomes invariant for external uncontrolled influence in static mode.

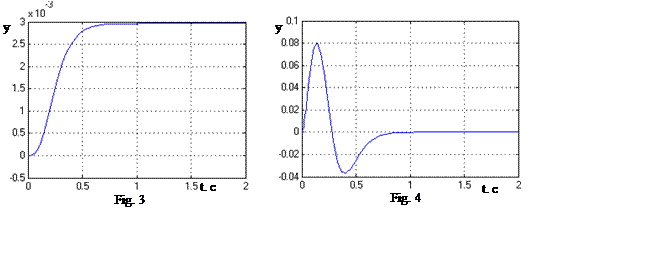
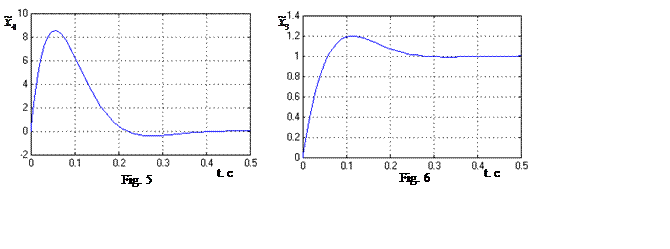
The results of simulation in MATLAB worked up system with  and  are introduced in Fig. 3, 4 (Fig. 3 – input influence, Fig. 4 - external uncontrolled influence). In Fig. 5, 6 are introduced estimate errors of immeasurable state-variables  when external uncontrolled influence is entered. These estimate errors confirms rightly got results.

3. conclusion

The approach under consideration is oriented on determine systems and determine influences. The results of this work allow to give some recommendations, when an closed-loop system with observer is created. First of all it should be analyzed additional observer properties, and only after that, if it is necessary, traditional method of suppression external uncontrolled influence should be used. This research shows the rationality for obtained results using for high order objects with alternation measurable and immeasurable state variables. Constructing sub observers with low order with special structure may considerably simplify finding effective control laws.

4. references

[1] Andrievsky B. R., Fradkov A.L. Selected chapters of control theory with MATLAB examples. St. Peterburg: Nauka, 1999. – 467 p. (series “Analyses and Design of Nonlinear Systems”).

[2] Pervozvansky A. A. Course of  automatic control theory. St. Peterburg: Nauka, 1986. – 616 p.

[3] Luenberger D. G., “An Introduction to Observers,” IEEE Transactions on Automatic Control, Vol. AC-16, No 6, Dec. 1971 – 602 p.