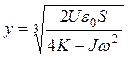Specification of some micromechanical gyro characteristics on basis of its design, страница 2

                                                        (8)

As it follows from equation (8) 5 parameters are needed to calculate a gap. Manufacturing flaws affection on S and J is much less than on parameters of elastic suspension, so their values may be considered as constants. Manufacturing errors of geometrical parameters of elastic suspension affect the mechanical spring K_mech, which is a part of the K in eq. (8). Therefore, to define the gap and considering two variables (y and K) in the eq. (8) unknown, two measures of the y-axis resonant frequency need to be done. The resonant frequency may be measured with the method of generation of auto-oscillations.

Capacitance-rotation angle dependence 

Coriolis acceleration may be recalculated to disc rotation angle if spring constant, Q-factor and difference between resonant frequencies of oscillations around x and y-axis are known.

The angular motion of the disc around the y-axis is measured by capacitive pickups shown in fig.4. A capacitance calculation program was created with the ANSYS program.

Nominal gap value is 2mkm (fig.5). Expected variation of this parameter is 20% i.e. (2.0 ± 0.4)mkm. Angle variation value was set to provide 1.5mkm deviation of the electrode in both directions. Thus angle variation value was from -0.06 to +0.06 deg.

Approximating curve of the dependence is shown in fig.6a.

The best approximation function for this dependence is given:

 with coefficients:                                    (9)

where x is Alpha (angle of the electrode deviation) and y is capacitance between the electrode and the disc. Standard deviation of function (9) is about 0.00084529 pF. In fig.6b we can see that maximum deviation of the approximation function is not more than 0,002195 pF. Therefore precision of estimate of the dependence is 0.03%.

In fig.6a is shown the capacitance-angle dependence calculated for one pair of electrodes as it shown in fig.4b. In fact in MMG there are two pairs of such electrodes, as it schematically shown in fig.5. Such a capacitive pickup is called a differential capacitive pickup. Capacitance of the differential pickup is given (fig.7a):

,                                       (10)

For estimation of the errors due to manufacturing defects the capacitance-angle dependence was calculated at variation of the gap from 1.6mkm to 2.4mkm. There is an example in fig.7a: for the C=10pF at the variation of the gap the angle may be from 0.05 to 0.06 deg.

Capacitance dependence on two parameters: the disc rotation angle and the gap for the differential capacity pickup is shown in fig. 7b. This dependence also may be approximated by the following function:

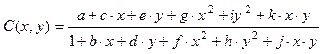                         (11)

where x is Alpha and y is gap, and а, b, c, d, e, f, g, h, i, j, k are coefficients of the function.

Therefore for precise estimation of the output of the MMG the precise value of the gap need to be known.

Conclusion

Defining the resonant frequency of the oscillations around y-axis the correction for “negative” spring must be considered. The gap between the disc and the electrode may be defined experimentally with the proposed method. Proposed capacity-disc rotation angle dependence allows defining nonlinearity and sensitivity of MMG without using a rotary table, i.e. allows reducing time and hence cost of defining these parameters of MMG.

References

1.   В.Г.Пешехонов, Л.П.Несенюк, С.Г.Кучерков, М.И.Евстифеев, Я.А.Некрасов и др. Результаты разработки микромеханического гироскопа/XII С.-Петербургская межд. конф. по интегрированным навигац. системам. – С.-Петербург: ЦНИИ «Электроприбор», 2005.

2.  William A. Clark, Thor Juneau, Roger T. Howe. Micromachined vibratory rate gyroscope. USA patent № 6,067,858