, (1.11)
where 
are expansion coefficients, found with formulas
, 
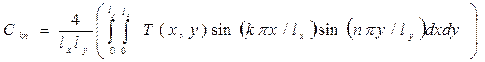. (1.12)
The
formulas (1.9) and (1.11) allow to introduce transfer function of distributed
control object with eigenfunction or 
- constituents
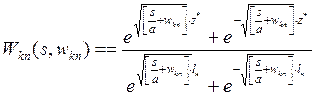, (1.13)
where 
is generalized coordinate.
2. FREQUENCY CHARACTERISTICS
On the basis of formula (1.13) it is possible to determinate logarithmic frequency characteristics of distributed control object
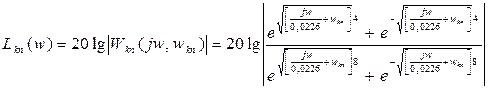
(2.1)
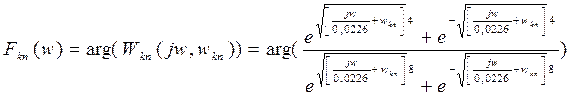
(2.2)
The formulas (2.1) and (2.2) describe logarithmic amplitude-frequency characteristic and logarithmic phase-response characteristic conformably. The mentioned below figures represent forms of the frequency characteristics:
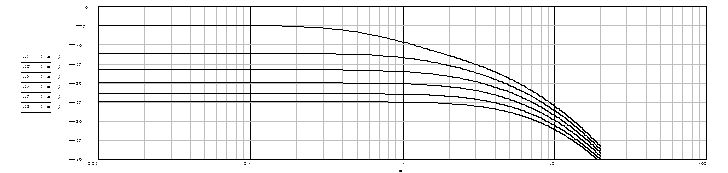Fig. 2.1. Logarithmic
amplitude-frequency characteristic with different value of
.
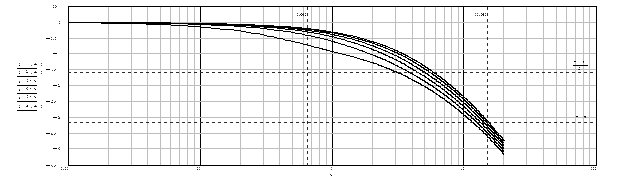
Fig.2.2. Logarithmic phase-response
characteristic with different value of .
Controllable objects speed increasing of passing processes with control or constants changing may cause these control systems instability. Therefore during control systems design of it is important to provide stability with some stability factor [5]. For ensure control system necessary dynamic characteristics we choose necessary frequency characteristics in the follow way
.
(2.3)
The frequency
characteristics of sequential corrective units (fig. 2.3) is the result of subtraction
, 
from necessary frequency characteristics 
and 
Fig.2.3. Logarithmic amplitude-frequency characteristic of corrector.
3. THE DESIGNING OF CORRECTIVE UNIT
According to fig. 2.3 for ensuring correction it is necessary to provide dependence transfer constant upon generalized coordinate represented on fig. 2.4
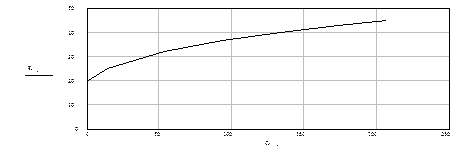
Fig.3.1. Dependence transfer constant 
upon generalized coordinate.
For this purpose
it is possible to use distributed – intensive unit which transfers function doesn’t
depend upon 
and represented by expression
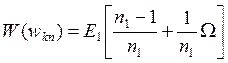, (3.1)
where 
is number (overall gain), 
,
are weighting coefficients (
), is generalized coordinate. On basis of (3.1) it is possibly to find
logarithmic amplitude-frequency characteristic of distributed – intensive unit
. (3.2)
Constants 
and 
in formula (3.2) are found so that the curve on fig. 3.1 to
approximate by formula (3.2) in the best way. In this report mentioned constants
are found with modeling. Mentioned below logarithmic amplitude-frequency
characteristic is with 
and 
.
Fig. 3.2. Approximate 
.
Today the most convenient way to incarnate corrective units is realization with computer. Let spatial and temporal variables represented with discontinuous values:
, 
, 
, 
, (3.3)
where 
; 
; 
, but 
, 
, 
and 
are given numbers which choose so that
necessary approximation precision of continuous function 
and 
by discontinuous values is ensued:
, (3.4)
where 
is given distribution law of temperature in the furnace working place.
Consideration with (3.3), (3.4) the second partial derivatives which accord with generalized coordinate determinate by approximate expression:
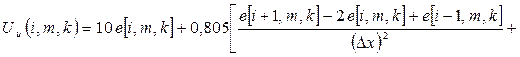
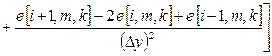, (3.5)
where 
is temperature deviation from given value.
The main result of this task is the realization of correctional element with synthesis frequency method algorithm model receiving. This found correctional element application gives an opportunity, from one hand, to increase the speed of transitional processes in the heat furnace, and from the other hand, to secure stability and required quality coefficients - a little overcorrection and variability.
The built control system may be used practically in all fields of industry, in which these or those thermal objects are applied.
REFERENCES
[1] A.A. Kolesnikov, Modern control theory, Taganrog : TSURE, 2000 (in Russian).
[2] A.R. Gayduk, Control system design algebraic methods, Rostov-on-Done : RSU (in Russian).
[3] A.V. Bezadze, Mathematic physic equations, Moscow : Nauka, 1990 (in Russian).
[4] H.O. Fattorini, Infinite Dimensional Optimization and Control Theory, 1998.
[5] Ogata, Modern Control Engineering, 3rd Ed. Prentice Hall, 1997.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.