Выбор керамических материалов для защиты от абразивной эрозии элементов газонефтяных трубопроводов, страница 2

Приведем пример решения уравнения (9) расчета α_лаб, исходя из значений параметров, взятых для первого варианта таблицы 1.

По формуле (10) находим F = 0,0024.

Запишем: sinα_лаб * (1- cos α_лаб) = 0,0024.

Выразим синус и косинус через тангенс половинного угла. Так как

sin x = 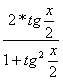, а cos x = ,

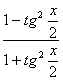то выражение примет следующий вид:

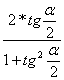* (1 - 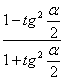) = 0,0024.

Произведем замену:

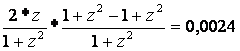
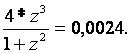
Получаем выражение вида:

Для решения кубического уравнения воспользуемся формулой Кардано.

Формула Кардано — формула для отыскания корней кубического уравнения вида y³ + py + q = 0 над полем комплексных чисел.

К такому виду может быть приведено любое кубическое уравнение

ax³ + bx² + cx + d = 0

при помощи следующей замены:

$x=y-\frac b{3a}$

$p=-\frac{b^2}{3a^2}+\frac{c}{a}$

$q=\frac{2b^3}{27a^3}-\frac{bc}{3a^2}+\frac{d}{a}$

Учитывая, что для нашего уравнения a=4, b=- 0,0024, c=0, d=- 0,0024,

производим замену:

z = y + 0,0024/12 = y + 0,0002

p =

q =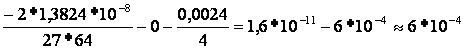

Запишем получившееся уравнение вида y³ + py + q = 0:

y³ – 0,12*10^-6*y – 6*10^-4 = 0

Формула Кардано имеет вид:

$y=\sqrt[3]{-{q\over 2}+ \sqrt{-\frac\Delta{108}}}+\sqrt[3]{-{q\over 2}- \sqrt{-\frac\Delta{108}}}$

где

1 2 3 4 5