Исследование задачи идентификации линейных стационарных динамических систем рекуррентным методом наименьших квадратов

Санкт-Петербургский Государственный Университет Информационных Технологий, Механики и Оптики

Кафедра Систем  Управления  и Информатики

Лабораторная работа № 3

" Идентификация линейных динамических систем "

по курсу "Идентификация и диагностика систем

Санкт-Петербург

2007 г.

Цель работы:исследование задачи идентификации линейных стационарных динамических систем рекуррентным методом наименьших квадратов.

Рассматриваются линейные стационарные объекты, описываемые уравнениями ВВ:

, где

 - входная последовательность,

 - выходная последовательность,

 - дискретное время.

Измерения выхода  производятся  в дискретные моменты времени  и сопровождаются аддитивными ошибками наблюдения, так что измеряемый выходной сигнал равен:

, где

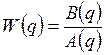 - дискретная передаточная функция объекта идентификации,

 - передаточная функция формирующего фильтра в канале помехи,

 - дискретный белый шум с параметрами (0,1),

 - оператор сдвига вперед.

Для оценки неизвестного параметра используется рекуррентный метод наименьших квадратов:

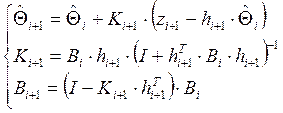
Изначально выбирается начальное значение  (случай отсутствия априорной информации) и  - достаточно большое положительное число.

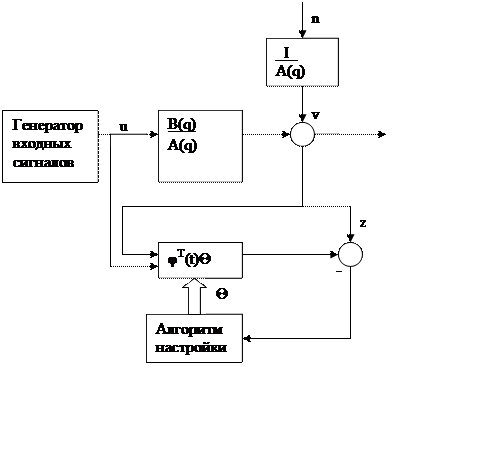
Схемамоделирования:

1. Детерминированное входное воздействие:

а) Дисперсия входного сигнала = 0

Дисперсия помехи = 0

Начальное b = 100000

Константа момента остановки = 0.000001

Вектор истинных значений TETA: [а1;…;аn] = [0.1; 0.2; 0.3]

Вектор истинных значений TETA: [b1;…;bn] = [1; 2; 3]

Результаты вычислений:

Оценка teta на t шаге = [0.099997; 0.2; 0.3; 0.99999; 2; 3]

Количество проделанных шагов = 9

График моделирования:

Q

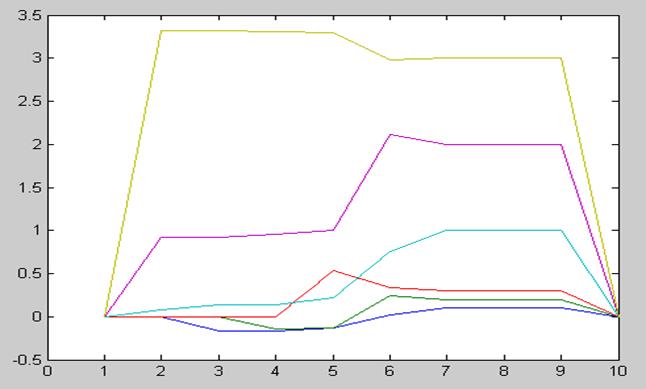
Ошибка оценки:

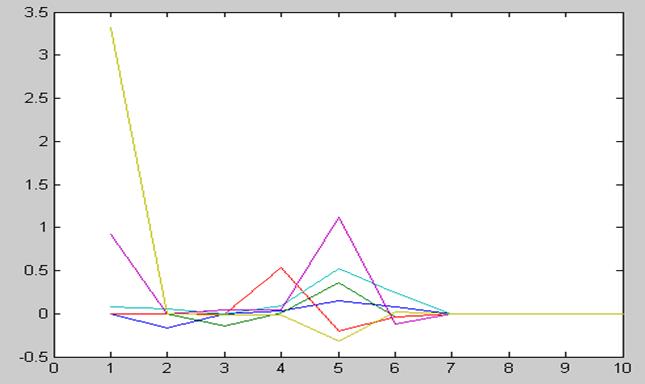M

б) Дисперсия входного сигнала = 1

Дисперсия помехи = 0

Начальное b = 100000

Константа момента остановки = 0.000001

Вектор истинных значений TETA: [а1;…;аn] = [0.1; 0.2; 0.3]

Вектор истинных значений TETA: [b1;…;bn] = [1; 2; 3]

Результаты вычислений:

Оценка teta на t шаге = [0.099997; 0.2; 0.3; 0.99999; 2; 3]

Количество проделанных шагов = 9

График моделирования:

Q

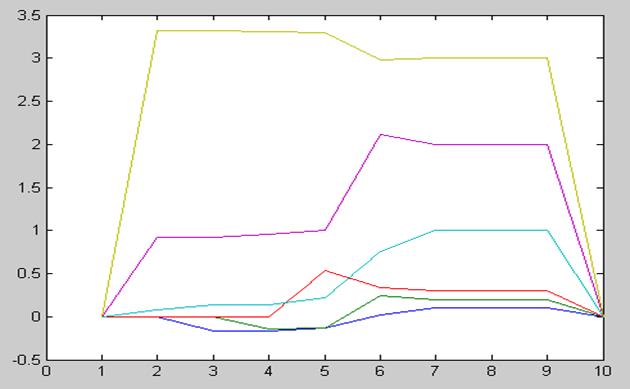
Ошибка оценки:

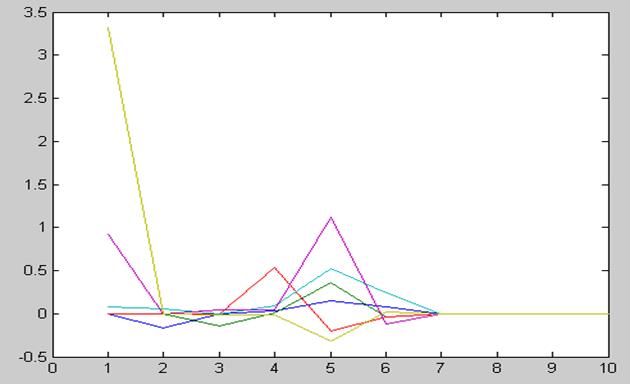M

в) Дисперсия входного сигнала = 0

Дисперсия помехи = 0.1

Начальное b = 100000

Константа момента остановки = 0.000001

Вектор истинных значений TETA: [а1;…;аn] = [0.1; 0.2; 0.3]

Вектор истинных значений TETA: [b1;…;bn] = [1; 2; 3]

Результаты вычислений:

Оценка teta на t шаге = [0.099997; 0.2; 0.3; 0.99999; 2; 3]

Количество проделанных шагов = 9

График моделирования:

Q

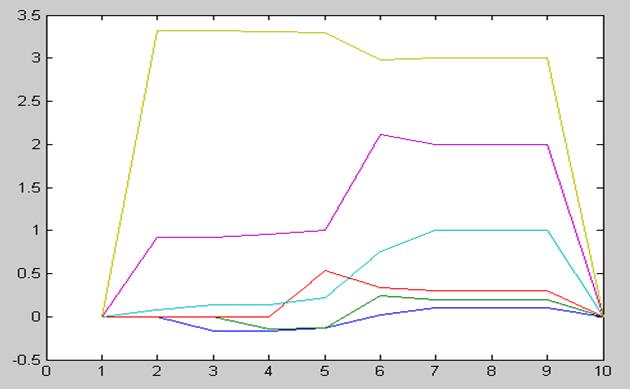
Ошибка оценки:

M

г) Дисперсия входного сигнала = 0

Дисперсия помехи = 0

Начальное b = 1000

Константа момента остановки = 0.000001

Вектор истинных значений TETA: [а1;…;аn] = [0.1; 0.2; 0.3]

Вектор истинных значений TETA: [b1;…;bn] = [1; 2; 3]

Результаты вычислений:

Оценка teta на t шаге = [0.099701; 0.20016; 0.29977; 0.99939; 2.0003; 2.9999]

Количество проделанных шагов = 19

График моделирования:

Q

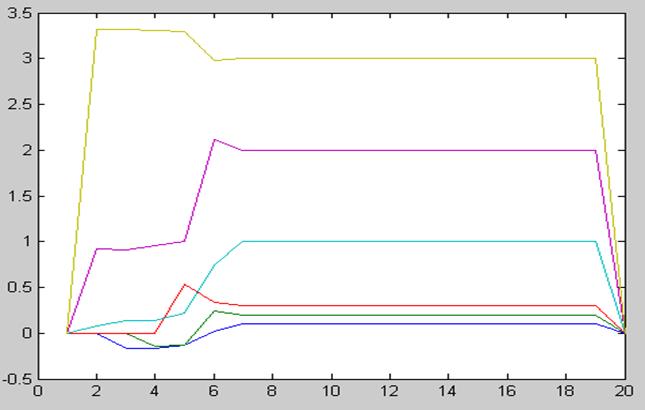
Ошибка оценки:

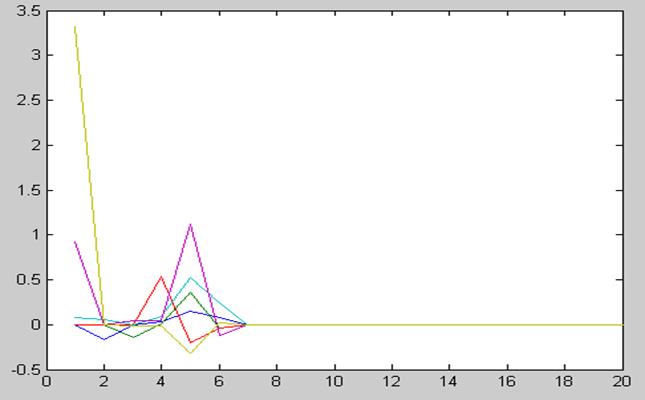M

д) Дисперсия входного сигнала = 0

Дисперсия помехи = 0

Начальное b = 1000000

Константа момента остановки = 0.001

Вектор истинных значений TETA: [а1;…;аn] = [0.1; 0.2; 0.3]

Вектор истинных значений TETA: [b1;…;bn] = [1; 2; 3]

Результаты вычислений:

Оценка teta на t шаге = [0.072129; 0.21405; 0.27801; 0.94321; 2.0261; 2.9952]

Количество проделанных шагов = 14

График моделирования:

Q

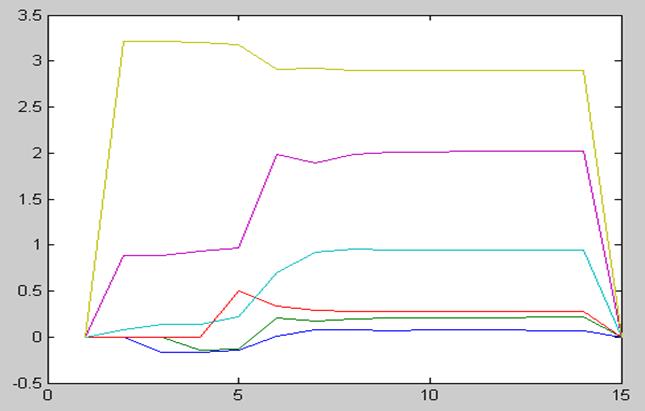
Ошибка оценки:

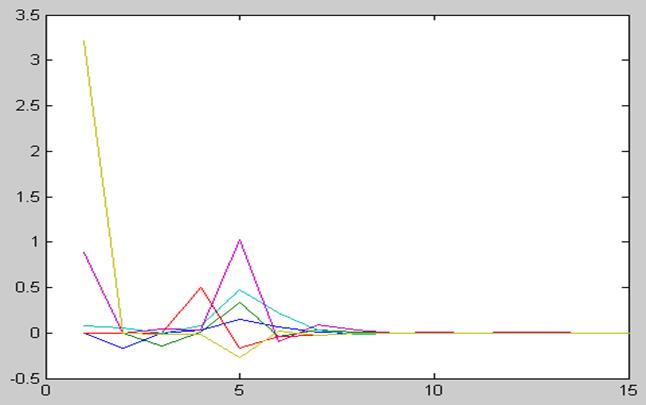M

2. Случайное входное воздействие

а) Дисперсия входного сигнала = 0.1

Дисперсия помехи = 0.1

Начальное b = 100000

Константа момента остановки = 0.000001

Вектор истинных значений TETA: [а1;…;аn] = [0.1; 0.2; 0.3]

Вектор истинных значений TETA: [b1;…;bn] = [1; 2; 3]

Результаты вычислений:

Оценка teta на t шаге = [0.099988; 0.20001; 0.3; 0.99996; 1.9999; 2.9999]

Количество проделанных шагов = 12

График моделирования:

Q

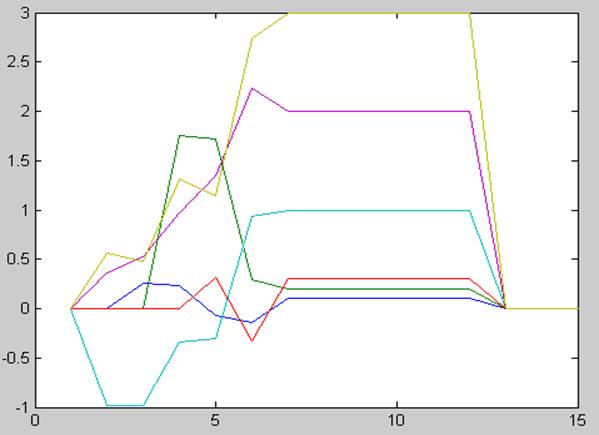
Ошибка оценки:

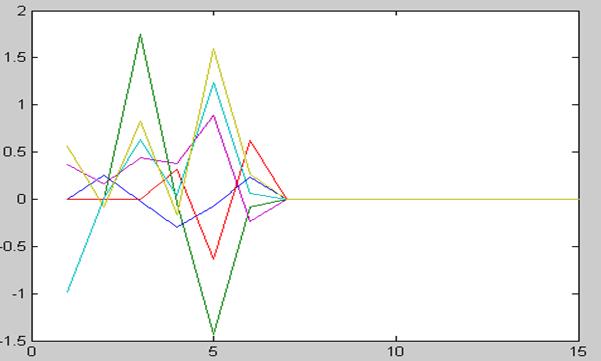M

б) Дисперсия входного сигнала = 0.5

Дисперсия помехи = 0.1

Начальное b = 100000

Константа момента остановки = 0.000001

Вектор истинных значений TETA: [а1;…;аn] = [0.1; 0.2; 0.3]

Вектор истинных значений TETA: [b1;…;bn] = [1; 2; 3]

Результаты вычислений:

Оценка teta на M шаге = [0.099996; 0.2; 0.3; 0.99999; 2; 3]

Количество проделанных шагов = 11

График моделирования:

Q

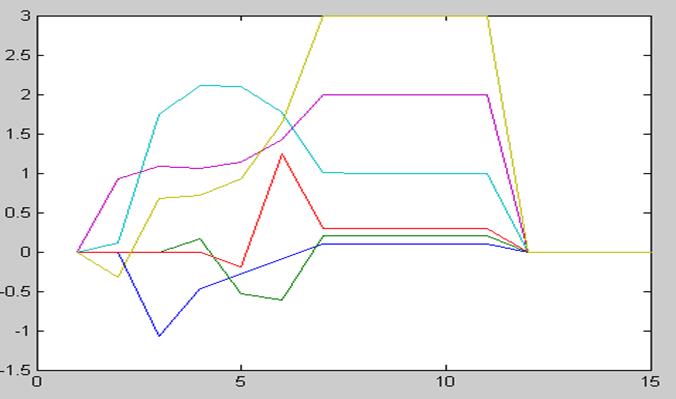
Ошибка оценки:

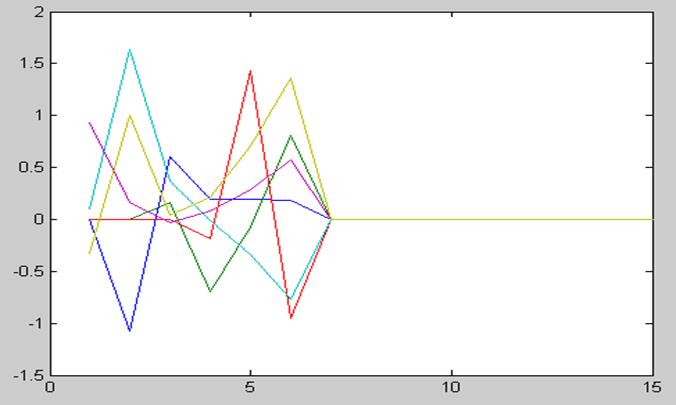M

в) Дисперсия входного сигнала = 0.1

Дисперсия помехи = 0.5

Начальное b = 100000

Константа момента остановки = 0.000001

Вектор истинных значений TETA: [а1;…;аn] = [0.1; 0.2; 0.3]

Вектор истинных значений TETA: [b1;…;bn] = [1; 2; 3]

Результаты вычислений:

Оценка teta на t шаге = [0.099995; 0.2; 0.3; 0.99999; 2; 3]

Количество проделанных шагов = 20

График моделирования:

Q

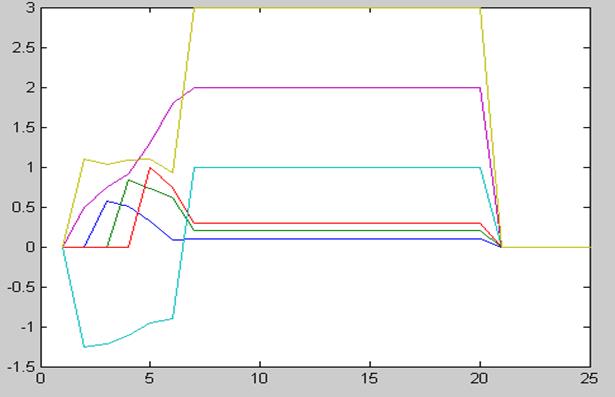
Ошибка оценки:

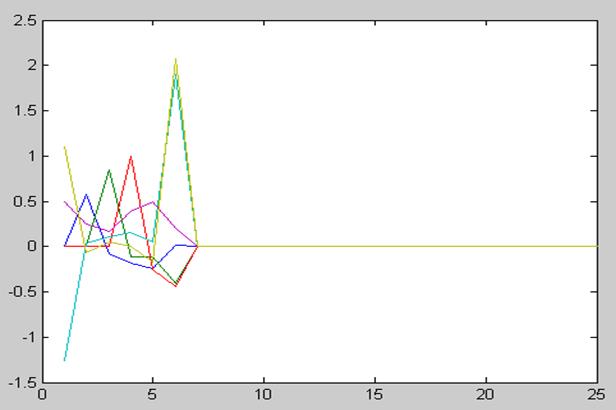M

г) Дисперсия входного сигнала = 0.1

Дисперсия помехи = 0.1

Начальное b = 1000

Константа момента остановки = 0.000001

Вектор истинных значений TETA: [а1;…;аn] = [0.1; 0.2; 0.3]

Вектор истинных значений TETA: [b1;…;bn] = [1; 2; 3]

Результаты вычислений:

Оценка teta на t шаге = [0.0998; 0.2; 0.29999; 0.99986; 1.9991; 2.9989]

Количество проделанных шагов = 43

График моделирования:

Q

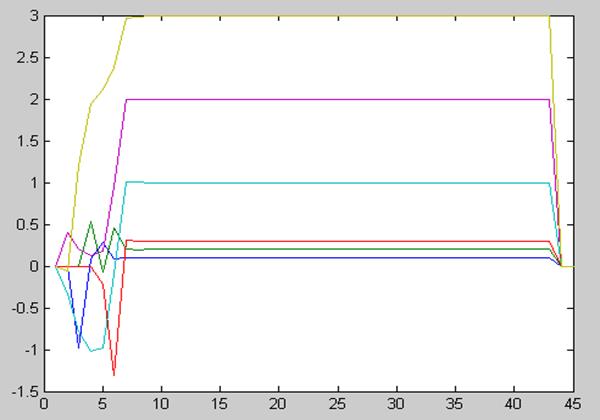
Ошибка оценки:

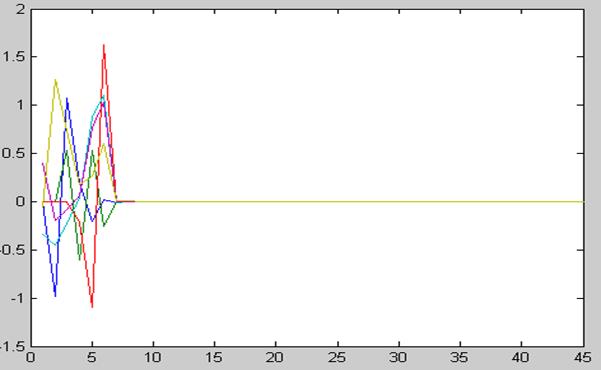M

д) Дисперсия входного сигнала = 0.1

Дисперсия помехи = 0.1

Начальное b = 100000

Константа момента остановки = 0.001

Вектор истинных значений TETA: [а1;…;аn] = [0.1; 0.2; 0.3]

Вектор истинных значений TETA: [b1;…;bn] = [1; 2; 3]

Результаты вычислений:

Оценка teta на t шаге = [0.099946; 0.20002; 0.29999; 0.99991; 2.001; 2.9997]

Количество проделанных шагов = 7

График моделирования:

Q

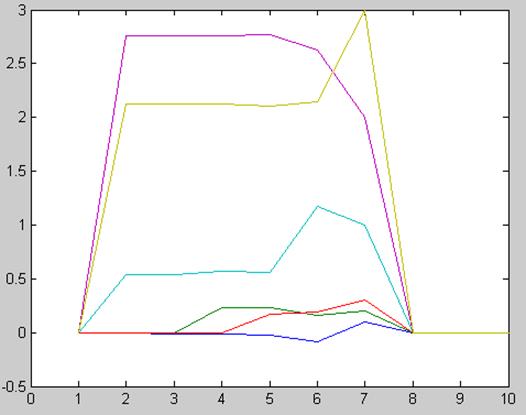
Ошибка оценки:

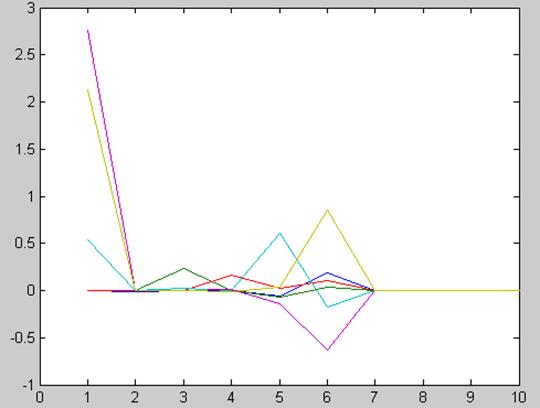M

Вывод: Как и в предыдущей работе мы воспользовались рекуррентным методом наименьших квадратов. Однако, на этот раз нами была рассмотрена не статическая, а стационарная динамическая система. Опыт показал, что для исследования  динамических систем большого числа шагов(как в статических системах) не требуется для оценки системы. Также следует отметить то, что оценка параметров в данном случае происходит с очень высокой точностью.