Исследование детерминированных процессов в системе самонаведения

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ

Кафедра радиотехнических систем

Отчет

по лабораторной работе №2

“ИССЛЕДОВАНИЕ ДЕТЕРМИНИРОВАННЫХ ПРОЦЕССОВ

В СИСТЕМЕ САМОНАВЕДЕНИЯ”

по курсу «Системы радиоуправления»

Выполнил ст. группы 041201 Типун И.Ф.

Проверил Демидович Г.Н.

Минск 2004

1. Цель работы:

а)исследование детерминированных процессов в системе самонаведения;

б)определить величину ошибки при статическом воздействии, при линейно изменяющемся воздействии и воздействии, изменяющемся по квадратичному закону.

2. Ход работы:

2.1. Изучение обобщенной функциональной схемы системы самонаведения

Функциональные   схемы   систем   самонаведения   различаются   видом координатора   (К),    устройством   формирования   команд   (УФК),   типом автопилота    (АП)    и    ракеты    (Р).    На   рис.1    приведена    обобщенная функциональная схема системы самонаведения.

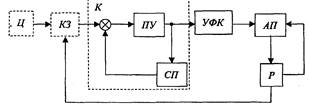
Рис. 1. Обобщенная функциональная схема системы самонаведения

В соответствии с функциональной схемой и математическими моделями входящих в нее динамических звеньев, составим структурную схему контура системы самонаведения по методу пропорционального сближения (рис. 2).

В структурной схеме учтены источник случайного воздействия - угловой шум цели nц(0, а также случайные возмущения в виде эквивалентного шума на выходе пеленгационного устройства nп(t) и аэродинамические возмущения n_a(t), действующие на ракету в полете, которые проявляются в виде случайных отклонений угла атаки.

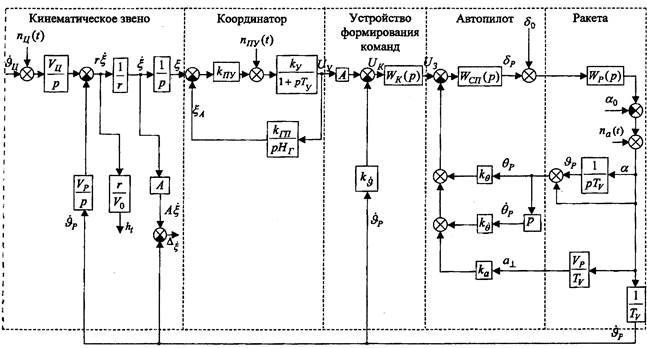
Рис. 2. Структурная схема контура системы самонаведения по методу пропорционального сближения

2.2. В среде MatLab собираем структурную схему контура самонаведения (рис.2.)

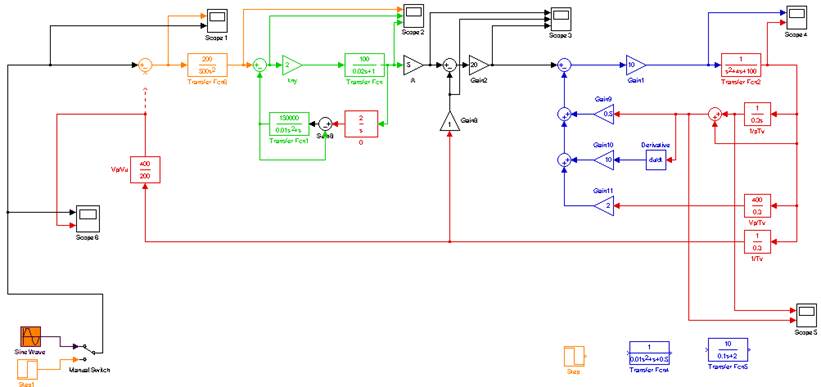
Рис.3. Структурная схема (устойчивая), собранная в среде MatLab

2.3. Проверка структурных схем на устойчивость (графический анализ)

№ сх	№ Scope	С ООС	Без ООС	Вывод
1	Scope 6			Не устойчива
2	Scope 6			Устойчива

Результаты были получены при задании в генераторе гармонического сигнала частотой f=20рад/с.

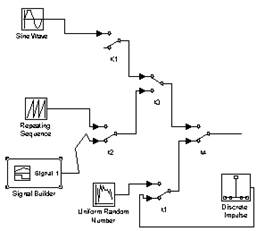
Рис.3.1. Реализация входного воздействия в виде математического представления

2.4. Снятие графических зависимостей в контрольных точках при воздействии на вход детерминированных процессов (ЛИН, квадратическое воздействие)

№ Scope	На вход воздействует ЛИН	На вход подается воздействие вида X2
Scope 1
Scope 2
Scope 3
Scope 4
Scope 5
Scope 6

2.5. Снятие графических зависимостей в контрольных точках при воздействии на вход детерминированных процессов (Единичное воздействие)

№ Scope	На вход подается единичное воздействие	На вход подается единичное воздействие длительностью 0,001 с
Scope 1
Scope 2
Scope 3
Scope 4
Scope 5
Scope 6

2.6. Получение передаточной функции системы путем математических преобразований структурной схемы в среде MatCad 2001i

Полученное уравнение является передаточной функцией все системы.

2.7. Построение переходной характеристики системы в среде MatLab v6.5

>>sys=tf([14222222,1422216888,213333332799999,79999999999],[0.53,82,8003395,432068998,167735185740,946602265899,122665711666666,46000000000,0])

Transfer function:

1.422e007 s^3 + 1.422e009 s^2 + 2.133e014 s + 8e010

-------------------------------------------------------------------------------------------------------------------------------------------0.53 s^8 + 82 s^7 + 8.003e006 s^6 + 4.321e008 s^5 + 1.677e011 s^4 + 9.466e011 s^3 + 1.227e014 s^2  + 4.6e010 s 

>>step(sys)

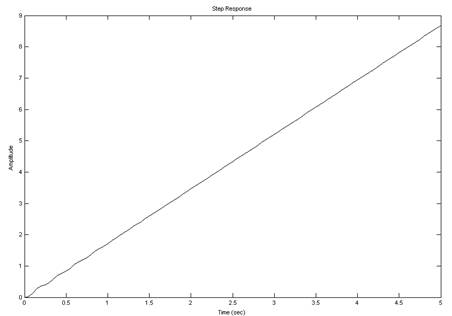
Рис.4. Переходная характеристика системы

2.8. Построение импульсной характеристики системы в среде MatLab v6.5

>>sys=tf([14222222,1422216888,213333332799999,79999999999],[0.53,82,8003395,432068998,167735185740,946602265899,122665711666666,46000000000,0])

Transfer function:

1.422e007 s^3 + 1.422e009 s^2 + 2.133e014 s + 8e010

-------------------------------------------------------------------------------------------------------------------------------------------0.53 s^8 + 82 s^7 + 8.003e006 s^6 + 4.321e008 s^5 + 1.677e011 s^4 + 9.466e011 s^3 + 1.227e014 s^2  + 4.6e010 s 

>>impulse(sys)

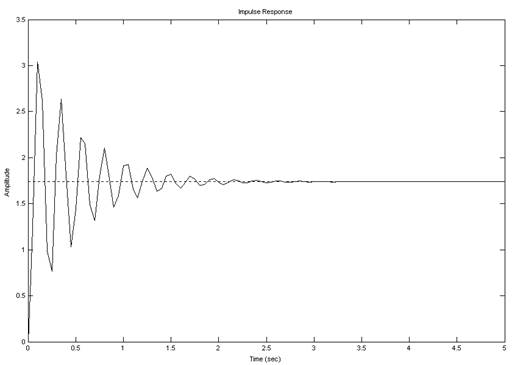
Рис.5. Импульсная характеристика системы

2.9. Построение годографа системы в среде MatLab v6.5

В командной строке MatLab`а вводим следующие  команды:

>>sys=tf([14222222,1422216888,213333332799999,79999999999],[0.53,82,8003395,432068998,167735185740,946602265899,122665711666666,46000000000,0])

Transfer function:

1.422e007 s^3 + 1.422e009 s^2 + 2.133e014 s + 8e010

-------------------------------------------------------------------------------------------------------------------------------------------0.53 s^8 + 82 s^7 + 8.003e006 s^6 + 4.321e008 s^5 + 1.677e011 s^4 + 9.466e011 s^3 + 1.227e014 s^2  + 4.6e010 s 

>> nyquist(sys)

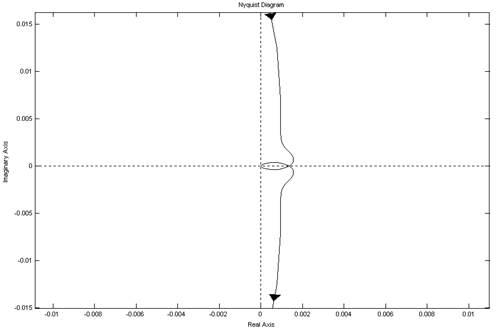
Рис 6. Годограф системы, построенный в среде MatLab v6.5

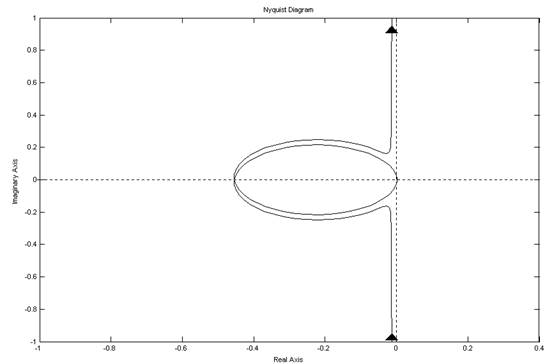
Рис 7. Годограф системы, построенный в среде MatLab v6.5 (увеличение  в 6 раз)

2.10. Построение АЧХ и ФЧХ системы в среде MatLab v6.5

В командной строке MatLab`а вводим следующие  команды:

>>sys=tf([14222222,1422216888,213333332799999,79999999999],[0.53,82,8003395,432068998,167735185740,946602265899,122665711666666,46000000000,0])

Transfer function:

1.422e007 s^3 + 1.422e009 s^2 + 2.133e014 s + 8e010

-------------------------------------------------------------------------------------------------------------------------------------------0.53 s^8 + 82 s^7 + 8.003e006 s^6 + 4.321e008 s^5 + 1.677e011 s^4 + 9.466e011 s^3 + 1.227e014 s^2  + 4.6e010 s 

>> bode(sys)

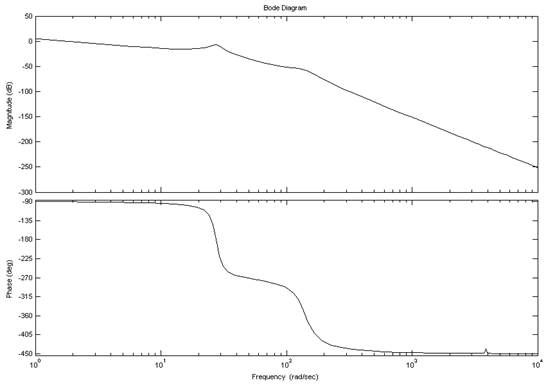
Рис.8.АЧХ и ФЧХ системы

2.11. Построение АЧХ ручным способом (поточечно)

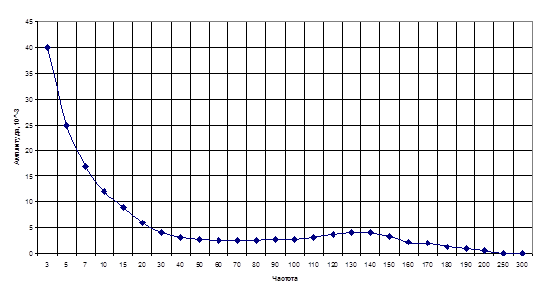
Рис.9. АЧХ системы